【文档说明】高考统考数学理科人教版一轮复习教师用书：第8章 第7节 抛物线 含解析【高考】.doc，共(19)页，469.500 KB，由小赞的店铺上传

转载请保留链接：https://www.doc5u.com/view-526e126d63cd5e8c65e99cc1380eb55c.html

以下为本文档部分文字说明：

-1-抛物线[考试要求]1.掌握抛物线的定义、几何图形、标准方程及简单几何性质(范围、对称性、顶点、离心率).2.理解数形结合思想.3.了解抛物线的实际背景及抛物线的简单应用．1．抛物线的定义满足以下三个

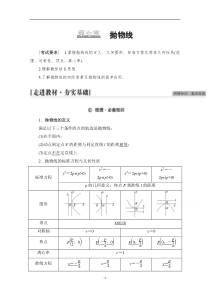
条件的点的轨迹是抛物线：(1)在平面内；(2)动点到定点F的距离与到定直线l的距离相等；(3)定点不在定直线上．2．抛物线的标准方程与几何性质标准方程y2＝2px(p>0)y2＝－2px(p>0)x2＝2py(p>0)x2＝－2py(p>0)p的几何意义：焦点F到准线l的距离图形顶点

O(0,0)对称轴y＝0x＝0焦点Fp2，0F－p2，0F0，p2F0，－p2离心率e＝1准线方程x＝－p2x＝p2y＝－p2y＝p2-2-范围x≥0，y∈Rx≤0，y∈Ry≥0，x∈Ry≤0，x∈R焦半径(

其中P(x0，y0))|PF|＝x0＋p2|PF|＝－x0＋p2|PF|＝y0＋p2|PF|＝－y0＋p2[常用结论]1．设AB是过抛物线y2＝2px(p＞0)焦点F的弦．(1)以弦AB为直径的圆与准线相切．(2)以AF或BF为直径的圆与y轴相切．(3)通径：过焦点垂直于

对称轴的弦，长等于2p，通径是过焦点最短的弦．2．过x2＝2py的准线上任意一点D作抛物线的两条切线，切点分别为A，B，则直线AB过点0，p2.一、易错易误辨析(正确的打“√”，错误的打“×

”)(1)平面内与一个定点F和一条定直线l的距离相等的点的轨迹一定是抛物线．()(2)若直线与抛物线只有一个交点，则直线与抛物线一定相切．()(3)方程y＝ax2(a≠0)表示的曲线是焦点在x轴上的抛物线，且其焦点坐标是a4，0，准线方程是x＝－a4.()(4)抛物线既是中心对称图形

，又是轴对称图形．()[答案](1)×(2)×(3)×(4)×二、教材习题衍生1．抛物线y＝14x2的准线方程是()A．y＝－1B．y＝－2C．x＝－1D．x＝－2A[∵y＝14x2，∴x2＝4y，∴准线方程为y＝－1.]2．若抛物线y＝4x2上的一点M到焦点的距离为1，则点M的

纵坐标是()A．1716B．1516C．78D．0-3-B[M到准线的距离等于M到焦点的距离，又准线方程为y＝－116，设M(x，y)，则y＋116＝1，∴y＝1516.]3．过抛物线y2＝4x的焦点的直线l交抛物线于P(x1，y1)，Q(x2，y2)两点，如果x1＋x2＝6

，则|PQ|等于()A．9B．8C．7D．6B[抛物线y2＝4x的焦点为F(1,0)，准线方程为x＝－1.根据题意可得，|PQ|＝|PF|＋|QF|＝x1＋1＋x2＋1＝x1＋x2＋2＝8.]4．已知抛物线的顶点是原点，对称轴为坐标轴，并且经

过点P(－2，－4)，则该抛物线的标准方程为．y2＝－8x或x2＝－y[设抛物线方程为y2＝2px(p≠0)或x2＝2py(p≠0)．将P(－2，－4)代入，分别得方程为y2＝－8x或x2＝－y.]考点一抛物线的定义及其应用抛物线定义的应用(1)利用抛物线的定义解决问题，应灵活地进行抛

物线上的点到焦点的距离与到准线距离的等价转化．即“看到准线想到焦点，看到焦点想到准线”．(2)注意灵活运用抛物线上一点P(x，y)到焦点F的距离|PF|＝|x|＋p2或|PF|＝|y|＋p2.[典例1](1)(2020·全国卷Ⅰ)已知A为抛物线C：y2＝2px(p>0)上一点，

点A到C的焦点的距离为12，到y轴的距离为9，则p＝()A．2B．3C．6D．9(2)设P是抛物线y2＝4x上的一个动点，若B(3,2)，则|PB|＋|PF|的最小值为．-4-(1)C(2)4[法一：因为点A到y轴的距离为9，所以可设点A(9，yA)，所以y2A＝18p.又

点A到焦点p2，0的距离为12，所以9－p22＋y2A＝12，所以9－p22＋18p＝122，即p2＋36p－252＝0，解得p＝－42(舍去)或p＝6.故选C．法二：根据抛物线的定义及题意得，点A到C的准线x＝－p2的距离为12，因为点A到

y轴的距离为9，所以p2＝12－9，解得p＝6.故选C．(2)如图，过点B作BQ垂直准线于点Q，交抛物线于点P1，则|P1Q|＝|P1F|.则有|PB|＋|PF|≥|P1B|＋|P1Q|＝|BQ|＝4，即|PB|＋|PF

|的最小值为4.][母题变迁]1．若将例(2)中的B点坐标改为(3,4)，试求|PB|＋|PF|的最小值．[解]由题意可知点B(3,4)在抛物线的外部．∵|PB|＋|PF|的最小值即为B，F两点间的距离，F(1

,0)，∴|PB|＋|PF|≥|BF|＝42＋22＝25，即|PB|＋|PF|的最小值为25.2．若将例(2)中的条件改为：已知抛物线方程为y2＝4x，直线l的方程为x－y＋5＝0，在抛物线上有一动点

P到y轴的距离为d1，到直线l的距离为d2，求d1＋d2的最小值．[解]由题意知，抛物线的焦点为F(1,0)．点P到y轴的距离d1＝|PF|－1，所以d1＋d2＝d2＋|PF|－1.易知d2＋|PF|的最小值为点F到直线l的距离，故d2＋|PF|的最小值为|1＋5|12＋(

－1)2＝32，所以d1＋d2的最小值为32－1.-5-点评：与抛物线有关的最值问题的转换方法(1)将抛物线上的点到准线的距离转化为该点到焦点的距离，构造出“两点之间线段最短”，使问题得解．(2)将抛物线上的点到焦点的距离转化为该点到准线的距离，利用“与直线上所有点的连线中

垂线段最短”原理解决．[跟进训练]1．已知F是抛物线y2＝x的焦点，A，B是该抛物线上的两点且|AF|＋|BF|＝3，则线段AB的中点到准线的距离为()A．52B．32C．1D．3B[∵F是抛物线y2＝x的焦点，∴F14，0，准线方程x＝

－14，设A(x1，y1)，B(x2，y2)，根据抛物线的定义可得|AF|＝x1＋14，|BF|＝x2＋14，∴|AF|＋|BF|＝x1＋14＋x2＋14＝3.解得x1＋x2＝52，∴线段AB中点的横坐标为54，∴线段AB的中点到准

线的距离为54＋14＝32.故选B．]2．已知动圆P与定圆C：(x－2)2＋y2＝1相外切，又与定直线l：x＝－1相切，那么动圆的圆心P的轨迹方程是()A．y2＝4xB．y2＝－4xC．y2＝8xD．y2＝－8xC[令

P点坐标为(x，y)，A(2,0)，动圆的半径为r，则根据两圆相外切及直线与圆相切的性质可得，|PA|＝1＋r，d＝r，P在直线的右侧，故P到定直线的距离是d＝x＋1，所以|PA|－d＝1，即(x－2)2＋y2－(x＋1)＝1，化简得y2＝8x.故选C．]考点二抛物线的标准方程及其性质-6-1

.求抛物线标准方程的方法(1)先定位：根据焦点或准线的位置．(2)再定形：即根据条件求p.2．抛物线性质的应用技巧(1)利用抛物线方程确定及应用其焦点、准线时，关键是将抛物线方程化成标准方程．(2)要结合图形分析，灵活运用平面图形的性质简化运算．[典例2](1)(2020·全国卷Ⅲ)设O为坐

标原点，直线x＝2与抛物线C：y2＝2px(p>0)交于D，E两点，若OD⊥OE，则C的焦点坐标为()A．14，0B．12，0C．(1,0)D．(2,0)(2)如图所示，过抛物线y2＝2px(p＞0)的焦点F的直线依次交抛物线及准线于点A，B，C，若|BC|＝2

|BF|，且|AF|＝4，则抛物线的方程为()A．y2＝8xB．y2＝4xC．y2＝2xD．y2＝x(1)B(2)B[(1)将直线方程与抛物线方程联立，可得y＝±2p，不妨设D(2,2p)，E(2，－2p)，由OD⊥OE，可得OD→·OE→＝4－4

p＝0，解得p＝1，所以抛物线C的方程为y2＝2x，其焦点坐标为12，0.故选B．(2)如图，分别过点A，B作准线的垂线，交准线于点E，D，设准线与x轴交于点G，设|BF|＝a，则由已知得|BC|＝2a，由定义得|BD|＝a，故∠BCD＝30°，-7-则在Rt△ACE中，

2|AE|＝|AC|，又|AF|＝4，∴|AC|＝4＋3a，|AE|＝4，∴4＋3a＝8，从而得a＝43，∵AE∥FG，∴FGAE＝CFAC，即p4＝48，p＝2.∴抛物线的方程为y2＝4x.故选B．]点评：在解决与抛物线的性质有关的

问题时，要注意利用几何图形形象、直观的特点来解题，特别是涉及焦点、顶点、准线的问题更是如此．[跟进训练]1．在平面直角坐标系xOy中，设抛物线y2＝4x的焦点为F，准线为l，P为抛物线上一点，PA⊥l，A为垂足．如果直线AF

的倾斜角为120°，那么|PF|＝.4[法一：抛物线y2＝4x的焦点为F(1,0)，准线方程为x＝－1.因为直线AF的倾斜角为120°，所以∠AFO＝60°.又tan60°＝yA1－(－1)，所以yA＝23.因为PA⊥l，所以yP＝

yA＝23.将其代入y2＝4x，得xP＝3，所以|PF|＝|PA|＝3－(－1)＝4.法二：抛物线y2＝4x的焦点为F(1,0)，准线方程为x＝－1.因为PA⊥l，所以|PA|＝|PF|.又因为直线AF的倾斜角为120°，所以∠AFO＝6

0°，所以∠PAF＝60°，所以△PAF为等边三角形，所以|PF|＝|AF|＝1－(－1)cos∠AFO＝4.]2．已知抛物线x2＝2py(p＞0)的焦点为F，点P为抛物线上的动点，点M为其准线上的动点，若△FPM为边长是4的等边三角形，则此抛物线的方程

为．x2＝4y[由△FPM为等边三角形，得|PM|＝|PF|，由抛物线的定义得PM垂直于抛物线的准线，设Pm，m22p，则点Mm，－p2，因为焦点F0，p2，△FPM是-8-等边三角形，所以m22p＋p2＝4，p2＋p22＋m

2＝4，解得m2＝12，p＝2，因此抛物线方程为x2＝4y.]考点三直线与抛物线的位置关系求解抛物线综合问题的方法(1)研究直线与抛物线的位置关系与研究直线与椭圆、双曲线的位置关系的方法类似，一般是用方程法，但涉及抛物线的弦长、中点、距离等问题时，要注意“设

而不求”“整体代入”“点差法”以及定义的灵活应用．(2)有关直线与抛物线的弦长问题，要注意直线是否过抛物线的焦点，若过抛物线的焦点，可直接使用公式|AB|＝x1＋x2＋p(焦点在x轴正半轴)，若不过焦点，则必须用弦长公式．提醒：涉及弦的中点、弦所在直线的斜率时一般

用“点差法”求解．[典例3](1)过点(0,1)作直线，使它与抛物线y2＝4x仅有一个公共点，这样的直线有条．(2)(2019·全国卷Ⅰ)已知抛物线C：y2＝3x的焦点为F，斜率为32的直线l与C的交点为A，B，与x轴的交点为P.①若|AF

|＋|BF|＝4，求l的方程；②若AP→＝3PB→，求|AB|.(1)3[结合图形分析可知(图略)，满足题意的直线共有3条：直线x＝0，过点(0,1)且平行于x轴的直线以及过点(0,1)且与抛物线相切的直线(非直线x＝0)．](2)[解]设直线l：y＝3

2x＋t，A()x1，y1，B()x2，y2.①由题设得F34，0，故|AF|＋|BF|＝x1＋x2＋32，由题设可得x1＋x2＝52.-9-由y＝32x＋ty2＝3x，可得9x2＋12(t－1)x＋4t2＝0，则x1＋x2＝－12(

t－1)9.从而由－12(t－1)9＝52，得t＝－78.所以l的方程为y＝32x－78.②由AP→＝3PB→得y1＝－3y2.由y＝32x＋t，y2＝3x，得y2－2y＋2t＝0.所以y1＋y2＝2

.从而－3y2＋y2＝2，故y2＝－1，y1＝3.代入C的方程得x1＝3，x2＝13.故|AB|＝4133.点评：解答本例(2)第②问的关键是从条件“AP→＝3PB→”中发现变量间的关系“y1＝－3y2”，从而为方程组的消元提供明确的方向．[跟进训练](2

017·全国卷Ⅰ)设A，B为曲线C：y＝x24上两点，A与B的横坐标之和为4.(1)求直线AB的斜率；(2)设M为曲线C上一点，C在M处的切线与直线AB平行，且AM⊥BM，求直线AB的方程．[解](1)设A(

x1，y1)，B(x2，y2)，则x1≠x2，y1＝x214，y2＝x224，x1＋x2＝4，于是直线AB的斜率k＝y1－y2x1－x2＝x1＋x24＝1.(2)由y＝x24，得y′＝x2.设M(x3，y3)，由题设知x32＝1，解得x3＝2，于是M(2,1)．-10-设直线

AB的方程为y＝x＋m，故线段AB的中点为N(2,2＋m)，|MN|＝|m＋1|.将y＝x＋m代入y＝x24得x2－4x－4m＝0.当Δ＝16(m＋1)>0，即m>－1时，x1,2＝2±2m＋1.从而|A

B|＝2|x1－x2|＝42(m＋1).由题设知|AB|＝2|MN|，即42(m＋1)＝2(m＋1)，解得m＝7.所以直线AB的方程为y＝x＋7.备考技法5活用抛物线焦点弦的四个结论抛物线的焦点弦问题一直是高考命题的一个热点，该问题常与弦长、三

角形面积、向量、不等式等知识相融合，考查学生的转化与化归意识和灵活解题能力．命题点主要体现在焦点弦的四个结论上：设AB是过抛物线y2＝2px(p＞0)焦点F的弦，若A(x1，y1)，B(x2，y2)，则(1)x1·x2＝p24.(2)y1·y2＝－p2.(3)|AB|＝x1＋x

2＋p＝2psin2α(α是直线AB的倾斜角)．(4)1|AF|＋1|BF|＝2p为定值(F是抛物线的焦点).[技法展示1]过抛物线y2＝4x的焦点F的直线l与抛物线交于A，B两点，若|AF|＝2|BF|，则|AB|等于()A．4B．92C．5D．6B[法一：(通性通法)易知直线l的斜率存在，设为

k，则其方程为y＝k(x－1)．由y＝k(x－1)，y2＝4x得k2x2－(2k2＋4)x＋k2＝0，得xA·xB＝1，①因为|AF|＝2|BF|，由抛物线的定义得xA＋1＝2(xB＋1)，-11-即xA＝2xB＋1，②由①②解得xA＝2，xB＝12，所以|AB|＝

|AF|＋|BF|＝xA＋xB＋p＝92.法二：(巧用结论)由对称性不妨设点A在x轴的上方，如图设A，B在准线上的射影分别为D，C，作BE⊥AD于E，设|BF|＝m，直线l的倾斜角为θ，则|AB|＝3m，由抛物线的定义知|AD

|＝|AF|＝2m，|BC|＝|BF|＝m，所以cosθ＝|AE||AB|＝13，所以tanθ＝22.则sin2θ＝8cos2θ，∴sin2θ＝89.又y2＝4x，知2p＝4，故利用弦长公式|AB|＝2psin2

θ＝92.法三：(巧用结论)因为|AF|＝2|BF|，所以1|AF|＋1|BF|＝12|BF|＋1|BF|＝32|BF|＝2p＝1，解得|BF|＝32，|AF|＝3，故|AB|＝|AF|＋|BF|＝92.][

评析]本例给出了三种解法，既有通性通法又有秒杀绝技，学习中要多总结，提升自己灵活解题的素养．[技法应用]如图，过抛物线y2＝2px(p＞0)的焦点F的直线交抛物线于点A，B，交其准线l于点C，若F是AC的中点，且|AF|＝4，则线段AB的长为()-12-A．5B．6C．163D

．203C[法一：(通性通法)如图，设l与x轴交于点M，过点A作AD⊥l交l于点D，由抛物线的定义知，|AD|＝|AF|＝4，由F是AC的中点，知|AD|＝2|MF|＝2p，所以2p＝4，解得p＝2，所以抛物线的方程

为y2＝4x.设A(x1，y1)，B(x2，y2)，则|AF|＝x1＋p2＝x1＋1＝4，所以x1＝3，可得y1＝23，所以A(3,23)，又F(1,0)，所以直线AF的斜率k＝233－1＝3，所以直线AF的方程为y＝3(x－1)，代入抛物线方程y

2＝4x得3x2－10x＋3＝0，所以x1＋x2＝103，|AB|＝x1＋x2＋p＝163.故选C．法二：(巧用结论)如上解得p＝2，设A(x1，y1)，B(x2，y2)，则|AF|＝x1＋p2＝x1＋1＝4，p＝2，所以x1＝3，又x1x2＝p24＝1，所以x2＝13

，所以|AB|＝x1＋x2＋p＝3＋13＋2＝163.法三：(巧用结论)因为1|AF|＋1|BF|＝2p，|AF|＝4，p＝2，所以|BF|＝43，所以|AB|＝|AF|＋|BF|＝4＋43＝163.]-13-[技法展示2]设F为抛物线C：y

2＝3x的焦点，过F且倾斜角为30°的直线交C于A，B两点，O为坐标原点，则△OAB的面积为()A．334B．938C．6332D．94D[法一：(通性通法)由已知得焦点坐标为F34，0，因此直线AB的方程为y＝33x－34，即4x－43y－3

＝0.与抛物线方程联立，化简得4y2－123y－9＝0，故|yA－yB|＝(yA＋yB)2－4yAyB＝6.因此S△OAB＝12|OF||yA－yB|＝12×34×6＝94.法二：(巧用结论)由2p＝3，及|AB|＝2psin2α，得|AB|＝2psin2α＝3sin230°

＝12.原点到直线AB的距离d＝|OF|·sin30°＝38，故S△AOB＝12|AB|·d＝12×12×38＝94.][评析]巧用结论解题避免了通性通法的繁杂计算．解题中务必熟记结论，灵活应用求解．结论：S△A

OB＝p22sinα，其中α为焦点弦AB的倾斜角．[技法应用](2020·成都模拟)O为坐标原点，F为抛物线C：y2＝4x的焦点，P为C上一点，若|PF|＝4，则△POF的面积为()A．2B．3C．2D．3

B[法一：(通性通法)由y2＝4x可得抛物线的焦点F(1,0)，准线方程为x＝－1，如图，过点P作准线x＝－1的垂线，垂足为M，根据抛物线的定义可知PM＝PF＝4，-14-设P(x，y)，则x－(－1)＝4，解得x＝3，将x＝3代入y

2＝4x可得y＝±23，所以△POF的面积为12|y||OF|＝12×23×1＝3.故选B．法二：(巧用结论)设∠PFx＝θ，则|PF|＝p1－cosθ＝21－cosθ＝4，∴cosθ＝12，即θ＝60°.设P(x，y)，则

|y|＝|PF|sinθ＝4×32＝23.∴S△POF＝12×|OF|×|y|＝12×1×23＝3.故选B．]备考技法6“设而不求”在解析几何中的妙用“设而不求”是解析几何解题简化运算的一种重要手段，它的精彩在于通过设出相应的参数，利用题设条件

加以巧妙转化，以参数为过渡，最大限度地减少运算；同时，“设而不求”也是比较特殊的一种思想方法，其实质是整体结构意义上的变式和整体思想的应用.活用定义，转化坐标[技法展示1]在平面直角坐标系xOy中，双曲线x2a2－y2b2＝1(a＞0，b＞0)的右支与焦点为

F的抛物线x2＝2py(p＞0)交于A，B两点，若|AF|＋|BF|＝4|OF|，则该双曲线的渐近线方程为．-15-y＝±22x[设A(xA，yA)，B(xB，yB)，由抛物线定义可得|AF|＋|BF|＝yA＋p2＋yB＋p2＝4×p2⇒yA＋y

B＝p，由x2a2－y2b2＝1，x2＝2py可得a2y2－2pb2y＋a2b2＝0，所以yA＋yB＝2pb2a2＝p，解得a＝2b，故该双曲线的渐近线方程为y＝±22x.][评析]设出点的坐标，先通过抛物线的定义，实现点的坐标与几何关系|AF|＋|BF|＝4|O

F|的转换，然后借助根与系数的关系建立参数a，b的等量关系，达到设而不求，从而求得双曲线的渐近线方程．[技法应用]抛物线y2＝4mx(m＞0)的焦点为F，点P为该抛物线上的动点，若点A(－m,0)，则|PF||PA|的最小值为．22[设点P的坐标

为(xP，yP)，由抛物线的定义，知|PF|＝xP＋m，又|PA|2＝(xP＋m)2＋y2P＝(xP＋m)2＋4mxP，则|PF||PA|2＝(xP＋m)2(xP＋m)2＋4mxP＝11＋4mxP(xP＋m)2≥11＋4mxP(2xP·m)2＝12(当且仅当xP＝m时取

等号)，所以|PF||PA|≥22，所以|PF||PA|的最小值为22.]妙用“点差法”，构造斜率[技法展示2]已知椭圆E：x2a2＋y2b2＝1(a＞b＞0)的右焦点为F(3,0)，过点F的直线交E于A，B两点．若AB的中点坐标为(1，－1)，则椭圆E的标准方程为()-1

6-A．x245＋y236＝1B．x236＋y227＝1C．x227＋y218＝1D．x218＋y29＝1D[设A(x1，y1)，B(x2，y2)，则x1＋x2＝2，y1＋y2＝－2，x21a2＋y21b2＝1，①x22a2＋y22b2＝1，②①－②得(x1＋x2)(x1－x2)a2

＋(y1＋y2)(y1－y2)b2＝0，所以kAB＝y1－y2x1－x2＝－b2(x1＋x2)a2(y1＋y2)＝b2a2.又kAB＝0＋13－1＝12，所以b2a2＝12.又9＝c2＝a2－b2，解得b2＝9，a2＝18，所以椭圆E的方程为x218＋y29＝1.][评析]该题目属

于中点弦问题，可设出A，B两点的坐标，通过“点差法”，巧妙地表达出直线AB的斜率，通过将直线AB的斜率“算两次”建立几何量之间的关系，从而快速解决问题．[技法应用]1．抛物线E：y2＝2x上存在两点关于直线y＝k(x－2)对称，则k的取值范围是．(－2，2)[当k＝0

时，显然成立．当k≠0时，设两对称点为B(x1，y1)，C(x2，y2)，BC的中点为M(x0，y0)，由y21＝2x1，y22＝2x2，两式相减得(y1＋y2)(y1－y2)＝2(x1－x2)，则直线

BC的斜率kBC＝y1－y2x1－x2＝2y1＋y2＝22y0＝1y0，由对称性知kBC＝－1k，点M在直线y＝k(x－2)上，所以y0＝－k，y0＝k(x0－2)，所以x0＝1.由点M在抛物线内，得y20<2x0，即(－k)2<2，所以－2<k<2，

且k≠0.综上，k的取值范围为(－2，2)．]-17-2．已知双曲线x2－y22＝1，过点P(1,1)能否作一条直线l与双曲线交于A，B两点，且点P是线段AB的中点？[解]假设存在直线l与双曲线交于A，B两点，且点P是线段AB的中点．设A(x1，y1)，B(x2，y2)，易知x

1≠x2，由x21－y212＝1，x22－y222＝1，两式相减得(x1＋x2)(x1－x2)－(y1＋y2)(y1－y2)2＝0，又x1＋x22＝1，y1＋y22＝1，所以2(x1－x2)

－(y1－y2)＝0，所以kAB＝y1－y2x1－x2＝2，故直线l的方程为y－1＝2(x－1)，即y＝2x－1.由y＝2x－1，x2－y22＝1，消去y得2x2－4x＋3＝0，因为Δ＝16－24＝－8<0

，方程无解，故不存在一条直线l与双曲线交于A，B两点，且点P是线段AB的中点．巧引参数，整体代入[技法展示3]已知椭圆x24＋y2＝1的左顶点为A，过A作两条互相垂直的弦AM，AN交椭圆于M，N两点．(1)当直线AM的斜率为1时，求点M的坐标；(2)

当直线AM的斜率变化时，直线MN是否过x轴上的一定点？若过定点，请给出证明，并求出该定点；若不过定点，请说明理由．[解](1)直线AM的斜率为1时，直线AM的方程为y＝x＋2，代入椭圆方程并化简得5x2＋16x＋12＝0.解得x1＝－2，x2＝－65，所以M－65，45.(2)设直

线AM的斜率为k，直线AM的方程为y＝k(x＋2)，-18-联立方程y＝k(x＋2)，x24＋y2＝1，化简得(1＋4k2)x2＋16k2x＋16k2－4＝0.则xA＋xM＝－16k21＋4k2，xM＝－xA－16k21＋4k2＝2－16k21＋4k2

＝2－8k21＋4k2.同理，可得xN＝2k2－8k2＋4.由(1)知若存在定点，则此点必为P－65，0.证明如下：因为kMP＝yMxM＋65＝k2－8k21＋4k2＋22－8k21＋4k2＋65＝5k4－4k2，同

理可计算得kPN＝5k4－4k2.所以直线MN过x轴上的一定点P－65，0.[评析]第(2)问先设出AM的方程为y＝k(x＋2)，联立方程，利用根与系数的关系求出xM，在此基础上借助kAM·kAN＝－1，整体代

入求出xN.[技法应用]已知F为抛物线C：y2＝2x的焦点，过F作两条互相垂直的直线l1，l2，直线l1与C交于A，B两点，直线l2与C交于D，E两点，求|AB|＋|DE|的最小值．[解]法一：由题意知，直线l1，l2的斜率都存在且不为0，F

12，0，设l1：x＝ty＋12，则直线l1的斜率为1t，联立方程得y2＝2x，x＝ty＋12，消去x得y2－2ty－1＝0.设A(x1，y1)，B(x2，y2)，则y1＋y2＝2t，y1y2＝－1.所以|AB|＝t2＋1|y1－y2|＝t2＋1·(y1＋y2)2－4y1y2＝t2

＋1·4t2＋4＝2t2＋-19-2，同理得，用1t替换t可得|DE|＝2t2＋2，所以|AB|＋|DE|＝2t2＋1t2＋4≥4＋4＝8，当且仅当t2＝1t2，即t＝±1时等号成立，故|AB|＋|DE|的最小值

为8.法二：由题意知，直线l1，l2的斜率都存在且不为0，F12，0，不妨设l1的斜率为k，则l1：y＝kx－12，l2：y＝－1kx－12.由y2＝2x

，y＝kx－12，消去y得k2x2－(k2＋2)x＋k24＝0，设A(x1，y1)，B(x2，y2)，则x1＋x2＝1＋2k2.由抛物线的定义知，|AB|＝x1＋x2＋1＝1＋2k2＋1＝2＋2k2.同理可得，用－1k替换|AB|中k，可得|DE|＝2＋2

k2，所以|AB|＋|DE|＝2＋2k2＋2＋2k2＝4＋2k2＋2k2≥4＋4＝8，当且仅当2k2＝2k2，即k＝±1时等号成立，故|AB|＋|DE|的最小值为8.