【文档说明】2023届数学一轮复习函数与导数：16.极值点偏移：判定定理【高考】.docx，共(6)页，518.324 KB，由小赞的店铺上传

转载请保留链接：https://www.doc5u.com/view-4ac8d4cb77f8dfb53fc103252359972e.html

以下为本文档部分文字说明：

1第16讲：极值点偏移判定定理一、极值点偏移的判定定理对于可导函数()yfx=，在区间(,)ab上只有一个极大（小）值点0x，方程()0fx=的解分别为1x，2x，且12axxb，（1）若102()(2)fxfxx−，则120()2xxx+，

即函数()yfx=在区间12(,)xx上极（小）大值点0x右（左）偏；（2）若102()(2)fxfxx−，则120()2xxx+，即函数()yfx=在区间12(,)xx上极（小）大值点0x右（左）偏.证明：（1）因为对于可导函数()yfx=，在区间(,

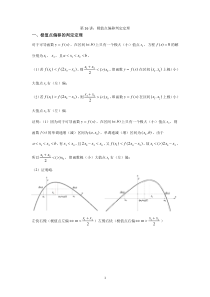
)ab上只有一个极大（小）值点0x，则函数()fx的单调递增（减）区间为0(,)ax，单调递减（增）区间为0(,)xb，由于12axxb，有10xx，且0202xxx−，又102()(2)fxfxx−，故102()2xxx−，所以120()2

xxx+，即函数极（小）大值点0x右（左）偏；（2）证明略.左快右慢（极值点左偏122xxm+）左慢右快（极值点右偏122xxm+）2左快右慢（极值点左偏122xxm+）左慢右快（极值点右偏122xxm+

）二、运用判定定理判定极值点偏移的方法1.方法概述：（1）求出函数()fx的极值点0x；（2）构造一元差函数00()()()Fxfxxfxx=+−−；（3）确定函数()Fx的单调性；（4）结合(0)0F=，判断()Fx的符号，从而确定0()fxx+、0()fxx−的大小关系

.口诀：极值偏离对称轴，构造函数觅行踪；四个步骤环相扣，两次单调紧跟随.2.抽化模型答题模板：若已知函数()fx满足2()()1fxfx=，0x为函数()fx的极值点，求证：1202xxx+.（1）

讨论函数()fx的单调性并求出()fx的极值点；假设此处()fx在0(,)x−上单调递减，在0(,)x+上单调递增.（2）构造00()()()Fxfxxfxx=+−−；注：此处根据题意需要还可以构造成0()()()Fxfxf2xx=−−的形式.（3）通过求导()Fx讨论(

)Fx的单调性，判断出()Fx在某段区间上的正负，并得出0()fxx+与0()fxx−的大小关系；假设此处()Fx在(0,)+上单调递增，那么我们便可得出000()()()()0FxFxfxfx=−=，从而得到：0xx时，00()()fxxfx

x+−.3（4）不妨设102xxx，通过()fx的单调性，12()()fxfx=，0()fxx+与0()fxx−的大小关系得出结论；接上述情况，由于0xx时，00()()fxxfxx+−且102xxx，12()()fxfx=，故1202002002()(

)[()][()](2)fxfxfxxxfxxxfxx==+−−−=−，又因为10xx，0202xxx−且()fx在0(,)x−上单调递减，从而得到1022xxx−，从而1202xxx+得证.（5）若要证明

1202xxf+，还需进一步讨论122xx+与0x的大小，得出122xx+所在的单调区间，从而得出该处函数导数值的正负，从而结论得证.此处只需继续证明：因为1202xxx+，故1202xxx+，由于()fx在0(,)x−上单调递减，故1202xxf+.【

说明】（1）此类试题由于思路固定，所以通常情况下求导比较复杂，计算时须细心；（2）此类题目若试题难度较低，会分解为三问，前两问分别求()fx的单调性、极值点，证明0()fxx+与0()fxx−（或()fx与0()f2xx−）的大小关系；若试题难度较大，则直接给出形如1202

xxx+或1202xxf+的结论，让你给予证明，此时自己应主动把该小问分解为三问逐步解题.1.已知函数()()xfxxexR−=.（Ⅰ）求函数()fx的单调区间与极值；（Ⅱ）若12xx，且12()()fxfx=，证明：122xx+.解析：（Ⅰ）由()()'1xfxxe−=−

，易得()fx的单调增区间为(),1−，单调减区间为()1,+，函数()fx在1x=处取得极大值()1f，且()11fe=（Ⅱ）由()()12fxfx=，12xx，不妨设12xx，则必有1201xx，4构造函数()()()

11Fxfxfx=+−−，(0,1x，则()()()''1'1Fxfxfx=++−()2110xxxee+=−，所以()Fx在(0,1x上单调递增，()()00FxF=，也即()()11fxfx+−对(0,1x恒成立.由1201xx，则(110,1x−，所以()()11

1fx+−=()()()11211fxfx−−−()()12fxfx==，即()()122fxfx−，又因为12x−，()21,x+，且()fx在()1,+上单调递减，所以122xx−，即

证122xx+.2.函数434()3fxxx=−与直线13yaa=−交于()1,Axa、()2,Bxa两点.证明：122xx+.解析：设12xx，函数434()3fxxx=−的单调递

减区间为(,1)−，单调递增区间为(1,)+，有21x，设()(1)(1)Fxfxfx=+−−，()2()83210Fxxx=−+，故()Fx单调递增区间为(,)−+，又(0)0F=，所以当0x时，()(0)0FxF=，即0x时，(

1)(1)fxfx+−，()()()()()1222112fxfxfxfx==+−−，又11x，221x−，又函数434()3fxxx=−单调递减区间为(,1)−，所以122xx−，即122xx+.53.已知函数2()lnfxxx=+，若12xx，且12()()fxfx=，证明

：124xx+.解析：由题意，函数2()lnfxxx=+的定义域为(0,)+，且22212()xfxxxx−=−+=，当(0,2)x时，()0fx，函数()fx单调递减；当(2,)x+时，()0fx，函数()fx单调递增，若1

2()()fxfx=，则必有122xx，所以142x−，而11111122()(4)lnln(4)4fxfxxxxx−−=+−+−−，令22()lnln(4)4hxxxxx=−++−−，则2222222222112(4)2(4)(4)'()(4)4(4)xxxxxxhxxxxxxx−−−

+−+−=−−++=−−−2228(2)0(4)xxx−=−−，所以函数()hx在(0,2)为减函数，所以()(2)0hxh=，所以11()(4)0fxfx−−，即11()(4)fxfx−，所以22()(4)fxfx−，所以124xx+.4.已知函数()()()221xfxxeax=

−+−有两个零点.设1x，2x是()fx的两个零点，证明：122xx+.解:因为()()()221xfxxeax=−+−'()(1)2(1)(1)(2)xxfxxeaxxea=−+−=−+．①设0a=，则()(2)xfxxe=−

，()fx只有一个零点．②设0a，则当(,1)x−时，'()0fx；当(1,)x+时，'()0fx．所以()fx在(,1)−单调递减，在(1,)+单调递增．又(1)ef=−，(2)fa=，取b满足0

b且ln2ab，则6223()(2)(1)()022afbbababb−+−=−，故()fx存在两个零点．③设0a，由'()0fx=得1x=或ln(2)xa=−．若2ea−，则ln(2)1a

−，故当(1,)x+时，'()0fx，因此()fx在(1,)+单调递增．又当1x时()0fx，所以()fx不存在两个零点．若2ea−，则ln(2)1a−，故当(1,ln(2))xa−时，'()0fx；当(ln(2),)xa−+时，'()0f

x．因此()fx在(1,ln(2))a−单调递减，在(ln(2),)a−+单调递增．又当1x时，()0fx，所以()fx不存在两个零点．不妨设12xx，由以上情况讨论知12(,1),(1,)xx−+，22(,

1)x−−，()fx在(,1)−单调递减，所以122xx+等价于()()122fxfx−，即2(2)0fx−．由于222222(2)(1)xfxxeax−−=−+−，而22222()(2)(1)0xfxxeax=−+−=，所以222222

(2)(2)xxfxxexe−−=−−−．设2()(2)xxgxxexe−=−−−，则2'()(1)()xxgxxee−=−−．所以当1x时，)'(0gx，而(1)0g=，故当1x时，()0gx．从而2

2()(2)0gxfx=−，故122xx+．