【文档说明】专题10 格点图问题（解析版）-备战2022年中考数学二轮专题归纳提升.docx，共(13)页，870.834 KB，由管理员店铺上传

转载请保留链接：https://www.doc5u.com/view-1fc529ea5e3ff6f8b58dada25570f70a.html

以下为本文档部分文字说明：

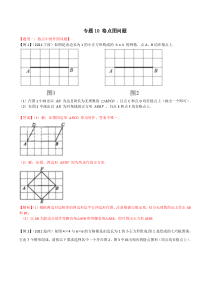
专题10格点图问题【题型一：格点中的作图问题】【例1】（2021·宁波）如图是由边长为1的小正方形构成的6×4的网格，点A，B均在格点上.（1）在图1中画出以𝐴𝐵为边且周长为无理数的▱𝐴𝐵𝐶𝐷，且点C和点D均在格点上（画出一个即可）.（2）在图2中画出以𝐴𝐵为对角线

的正方形𝐴𝐸𝐵𝐹，且点E和点F均在格点上.【答案】（1）解：如图四边形𝐴𝐵𝐶𝐷即为所作，答案不唯一.（2）解：如图，四边形𝐴𝐸𝐵𝐹即为所求作的正方形.【解析】（1）根据两边对边相等的四边形是平行四边形作图

，注意根据勾股定理，结合无理数的定义作出AD和BC；（2）以AB为斜边分别作等腰直角△AFB和等腰直角△AEB，即可得出正方形AEBF.【例2】（2021温州）如图4×4与6×6的方格都是由边长为1的小正方形组成.图1是绘成的七巧板图案，它由7个图

形组成，请按以下要求选择其中一个并在图2、图3中画出相应的格点图形（顶点均在格点上）.（1）选一个四边形画在图2中，使点P为它的一个顶点，并画出将它向右平移3个单位后所得的图形.（2）选一个合适的三角形，将它的各边长扩大到原来的√5倍，画在图3中.【答案】

（1）解：画法不唯一，当选四边形为正方形时可以是如图1或图2；当四边形式平行四边形时可以是图3或图4.（2）解：画法不唯一，当直角边长为√2时，扩大√5即直角边长为√10利用勾股定理画出直角边长为√10直角三角形可以是如

图5或图6当直角边长为2√2时，扩大√5即直角边长为2√10利用勾股定理画出直角边长为2√10直角三角形可以是如图7或图8等.【解析】（1）任选一个四边形，根据平移的性质分别得出对应点位置，然后将各点顺次连接起来即可；（2）先任选一个三角形，然后根据各边长扩大到原来的√5倍，得出每边的边长，最

后利用勾股定理在方格图中画出边长扩大后的三角形即可.【练1】如图①,②,③都是3×3的正方形网格,每个小正方形的顶点称为格点.A,B,C均为格点.在给定的网格中,按下列要求画图:(1)在图①中,画一条不与AB重合的线段MN,使MN与AB

关于某条直线对称,且M,N为格点.(2)在图②中,画一条不与AC重合的线段PQ,使PQ与AC关于某条直线对称,且P,Q为格点.(3)在图③中,画一个△DEF,使△DEF与△ABC关于某条直线对称,且D,E,F为格点.【答案】(1)如图①,MN即为所求(答案不唯一).(

2)如图②,PQ即为所求(答案不唯一).(3)如图③,△DEF即为所求(答案不唯一).【练2】如图,在所给的方格纸中,每个小正方形的边长都是1,点A,B,C位于格点处,请按要求画出格点四边形.(1)在图①中画出格点P,使AC

=CP,且以点A,B,C,P为顶点的四边形面积为3;(2)在图②中画出一个以点A,B,C,P为顶点的格点四边形,使AP2+CP2=15.【答案】(1)如图①中,四边形即为所求(答案不唯一).(2)如图②中,四边形即为所求(答案不唯一)【练3】如图，由5个大小完全相同的小正方形

摆成如图形状，现移动其中的一个小正方形，请在图（1），图（2），图（3）中分别画出满足以下各要求的图形．（用阴影表示）（1）使得图形既是轴对称图形，又是中心对称图形．（2）使得图形成为轴对称图形，而不是中心对称图形；

（3）使得图形成为中心对称图形，而不是轴对称图形．【答案】【题型二：格点中的计算问题】【例】如图,在5×5的正方形网格中,每个小正方形的边长为1,点A,B,C都在格点上,则cos∠BAC的值为.【答案】√55【解析】如图,找出格点D,E,连接CD,AD,易知△ACD是直角三角形,A,C

,E三点共线,连结BE,由勾股定理可知:AB2=1+9=10,AE2=1+1=2,BE2=4+4=8,∴AB2=AE2+BE2,∴△ABE是直角三角形,∴cos∠BAC=𝐴𝐸𝐴𝐵=√2√10=√55,故答案为√55

.【练1】如图,将正三角形ABC分割成m个边长为1的小正三角形和1个黑色菱形,这个黑色菱形可分割成n个边长为1的小正三角形.若𝑚𝑛=4725,则正三角形ABC的边长是.【答案】12【解析】设正三角形ABC的边长

为x,则高为√32x,∴S△ABC=12x·√32x=√34x2,∵所分成的都是边长为1的正三角形,∴结合图形可得黑色菱形的较长的对角线长为√32x-√3,较短的对角线长为√32x-√3√33=12x-1,∴黑色菱形的面积=12√32x-√3

12x-1=√38(x-2)2,∴𝑚𝑛=√34𝑥2-√38(𝑥-2)2√38(𝑥-2)2=4725,整理得11x2-144x+144=0,解得x1=1211(不符合题意,舍去),x2=12,所以,△ABC的边长是12.【练2】如图,在△ABC中,AB,BC,AC三边的长分

别为√2,√13,√17,求这个三角形的面积.小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC的三个顶点都在小正方形的顶点处),如图W5-9

①所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.(1)请你将△ABC的面积直接填写在横线上:.(2)我们把上述求△ABC面积的方法叫做构图法.若△ABC三边的长分别为2√2a,√10a,√26a(a

>0),请利用图②的正方形网格(每个小正方形的边长为a)画出相应的△ABC,并求出它的面积.(3)若△ABC三边的长分别为√𝑚2+4𝑛2,√𝑚2+16𝑛2,2√𝑚2+𝑛2(m>0,n>0,m≠n),请运用构图法在图③指定区域内画出示意图,并求出△ABC的面积.【答案】（1

）2.5（2）图见解析，S=4a2（3）图见解析，S=3mn【解析】（1）S△ABC=2×4-12×1×1-12×3×2-12×1×4=2.5,(2)如图,∵AB=2√2a,BC=√10a,AC=√26a,∴S△ABC=2a×5a-12×2a×2a-12×3a×a-1

2×a×5a=4a2.（3）如图,AB=√𝑚2+4𝑛2,AC=√𝑚2+16𝑛2,BC=2√𝑚2+𝑛2,∴S△ABC=2m×4n-12×2m×2n-12×m×4n-12×m×2n=3mn.【练3】如图,在5×5的正方形方格纸中,每个小正方形的边长为单位1,点A,B,C,P都在格点处

.(1)请在图中作△BCD,使△BCD是以CD为底的等腰三角形,且点D为格点.(2)在(1)的条件下,连结AD,则四边形ABCD的面积为,再连结AC,则tan∠ACD=.(3)请仅使用无刻度直尺在线段BC上作一点Q,使点Q满足∠P

QB=45°.(温馨提示:点Q可以是非格点哦!)【答案】（1）图见解析（2）10，13（3）图见解析【解析】（1）（2）如图，连接AD、AC四边形ABCD的面积=正方形ABMN的面积-三角形BMC的面积-三角形DNC的面积=4×4−12×2×

4−12×2×2=16−4−2=10由图可得，AC=BC（3）【题型三：格点中的计数问题】【例】如图,A,B是4×5网格中的格点,网格中的每个小正方形的边长是1,图中使以A,B,C为顶点的三角形是等腰三角形的格点C有几个？【答案】3个【解

析】如图，∵A,B是4×5网格中的格点,∴AB=√22+32=√13,同理可得AC=AE=BD=√13.∴所求三角形有:△ABD,△ABC,△ABE.【练1】如图,点A是5×5网格图形中的一个格点(小正方形的顶点),图中每个小正方形的

边长为1,以A为其中的一个顶点,面积等于52的格点等腰直角三角形(三角形的三个顶点都是格点)的个数为【答案】16个【解析】因为是面积等于52的格点等腰直角三角形,所以就要求直角边长为√5,如图,因为√5=√

12+22,所以以点A为圆心,√5为半径画圆,与格点的交点就是三角形的另一顶点,①当A位于直角顶点时,存在8种情况,如图①②.②当A位于斜边的一个顶点时,同样存在8种情况,如图③④.∴以A为顶点且面积等于52的格

点等腰直角三角形共有16个.【练2】在如图所示的5×5方格中，每个小方格都是边长为1的正方形，△ABC是格点三角形(即顶点恰好是正方形的顶点)，则与△ABC有一条公共边且全等的所有格点三角形的个数是．【答案】4个【解析】如图所示，以BC为公共边的三角形有3个，以AB为公共边的三角

形有0个，以AC为公共边的三角形有1个，总计4个.获得更多资源请扫码加入享学资源网微信公众号www.xiangxue100.com