【文档说明】《中考数学复习讲义》第六章 勾股定理 （二十七）——蚂蚁爬行模型.docx，共(8)页，797.191 KB，由管理员店铺上传

转载请保留链接：https://www.doc5u.com/view-1f51d838f51b763e488e0db5c6425707.html

以下为本文档部分文字说明：

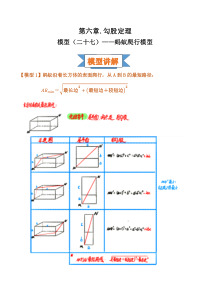
第六章.勾股定理模型（二十七）——蚂蚁爬行模型【模型1】蚂蚁沿着长方体的表面爬行，从A到B的最短路径：𝐴𝐵𝑚𝑖𝑛＝√最长边𝟐+(最短边＋较短边)𝟐模型讲解【模型2】蚂蚁沿着圆柱体的表面爬行，从A到B的最

短路径：①同测全周长＝√(2𝜋𝑟)2+ℎ2②异测半周长＝√(𝜋𝑟)2+ℎ2【模型3】蚂蚁吃蜂蜜问题∶求蚂蚁从A沿着外壁爬行再沿着内壁爬行到B的最短路径.【作法】如图，首先找到A关于杯子上沿的对称点

A′点，设A′到B的垂直距离为h，则问题转化为异侧半周长的问题.由图可知蚂蚁爬行的最短路径长为A´B＝√(𝜋𝑟)2+ℎ2典例1☆☆☆☆☆如图，长方体的长为15，宽为10，高为20，点B到点C的距离为5一

只蚂蚁如果要沿着长方体的表面从点A爬行到点B，则需要爬行的最短距离是________。【答案】25【解析】本题可看成蚂蚁是在长为5，宽为10，高为20的长方体表面爬行，根据蚂蚁沿长方体表面爬行的结论∶dmin＝√最长边𝟐+(最短边＋较短边)𝟐知dmin＝√𝟐�

�𝟐+(𝟏𝟎＋𝟓)𝟐＝25典例2☆☆☆☆☆如图，一圆柱高为8cm，底面半径为2cm，一只蚂蚁在圆柱侧面爬行，从点A爬到点B处觅食，则要爬行的最短路程（π取3）是（）口诀典例秒杀A.20cmB.1

0cmC.14cmD.无法确定【答案】B【解析】根据蚂蚁在圆柱表面爬行的结论，可知dmin＝√(𝜋𝑟)2+ℎ2＝√(3×2)2+82＝10(cm).典例3☆☆☆☆☆如图所示，圆柱形容器高为6cm，底面周长为6cm，在容器内壁离底部2cm的

点B处有一滴蜂蜜，此时一只蚂蚁正好在容器外壁，离容器上沿2cm与蜂蜜相对的点A处，则蚂蚁从外壁A处到达内壁B处的最短距离为______cm.【答案】3√5【解析】如图，将容器侧面展开，作A关于EF（容器上沿）的对称

点A´，连接A´B，过B作BC上FA于点C，A´B＝√(𝐴´𝐶)2+𝐵𝐶2＝√(6−2+2)2+32＝3√5（cm）.即蚂蚁从外壁A处到达内壁B处的最短距离为3√5cm.1.（★★★☆☆）如图是放在地面上的一个长方体盒子，其中AB=9cm，BC=6cm，BF=5cm，点M在棱AB上，

且AM＝3cm，N是FG的中点.一只蚂蚁要沿着长方体盒子的表面从点M爬行到点N，则它需要爬行的最短路程为（）A.10cmB.√106cmC.(6-√34)cmD.9cm2.（★★★☆☆）如图，正四棱柱的底面边长为5cm，侧棱长为6cm，

一只蚂蚁从四棱柱底面上的点A沿着棱柱表面爬到点C´处，求蚂蚁需要爬行的最短路径的长。1.如图是放在地面上的一个长方体盒子，其中AB=18cm，BC=12cm，BF=10cm，点M在棱AB上，且AM=6cm，N是FG的中点，一只蚂蚁要沿着长方体盒子的表

面从点M爬行到点N，则它需要爬行的最短距离为（)A.20cmB.2√106cmC.(12＋2√34)cmD.18cm蚂蚁爬行的最值问题是非常经典的一类最值问题，我们如果能够记住最值的特点，那么解题将会更

容易第六章.勾股定理模型（二十七）——蚂蚁爬行模型答案：小试牛刀1.答案A解析∵M，N之间的距离可以看作长、宽、高分别为6cm，3cm，5cm的长方体的对角顶点间的距离，所以根据蚂蚁沿长方体表面爬行的结论dmin＝√最长边𝟐+(最短边＋较短边)𝟐，

得dmin＝√𝟔𝟐+(𝟓＋𝟑)𝟐＝10（cm）.故选A.2.解析第一种情况∶当沿着平面ABB´A´、平面A´B´C´D´爬行时，其平面展开图如图所示，则AC´＝√(6+5)2+52＝√146（cm）.第二种情况∶当沿着平面ABB´A´、

平面BB´C´C爬行时，其平面展开图如图所示，则AC´＝√(5+5)2+62＝√136＝2√34（cm）.第三种情况∶当沿着平面ABCD、平面BB´C´C爬行时，与第一种情况路径长相同.因为2√34＜√146，所以蚂蚁需要爬行的最短路径的长是2√34cm.直击中考1.答案A

解析∵M，N之间的距离可以看作长、宽、高分别为12cm，6cm，10cm的长方体，∴根据蚂蚁在长方体表面爬行的结论dmin＝√最长边𝟐+(最短边＋较短边)𝟐边干较短边），得dmin＝√𝟏𝟐𝟐+(𝟏𝟎＋𝟔)𝟐＝20（cm）.故选A.