【文档说明】《中考数学二轮复习经典问题专题训练》专题53 与二次函数有关的综合问题（1）（解析版）.docx，共(25)页，656.521 KB，由管理员店铺上传

转载请保留链接：https://www.doc5u.com/view-08c63efeb219164c3b4234be0e053997.html

以下为本文档部分文字说明：

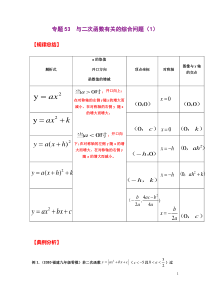
1专题53与二次函数有关的综合问题（1）【规律总结】解析式a的取值开口方向函数值的增减顶点坐标对称轴图像与y轴的交点时当0a；开口向上；在对称轴的左侧y随x的增大而减小，在对称轴的右侧y随x的增大而增大。时当0a；开口向下；在对称轴的左侧y随x的增大而增大，在对称

轴的右侧y随x的增大而减小。2)(hxay+=)44,22abacab−−（【典例分析】例1．（2020·福建九年级零模）若二次函数2yaxbxc=++（5c−且302a）过2yax=），（00），（0

0kax+=2y），（c0），（k0），（0h−0=x0=xhx−=khxay++=2)(），（kh−hx−=cbxaxy++=2abx2−=），（c0），（kah+20），（20ah2(,)Amn，()13,By，(2,)Cmn−，22,2Dy−

，()31,Ey，且AC到对称轴的距离相等0n，则1y，2y，3y的大小关系是（）A．312yyyB．321yyyC．123yyyD．312yyy【答案】B【分析】由点A（m，n）、C（2−m，n）到对称轴的距离相等，

可求函数的对称轴为x＝1，所以b=-2a，根据a、b和c的取值范围，可以判断3x=、22x=−和1x=时，函数2yaxbxc=++所对应的函数值312yyy，所以()13,By、22,2Dy−和()31,Ey所对应的的二次函数2

yaxbxc=++的函数值321yyy；【详解】∵点A（m，n）、C（2−m，n）到对称轴的距离相等，∴函数的对称轴为x＝1，∴b=-2a，又∵x=-1和x=3与对称轴的距离相等∴x=-1和x=3对应的函数值相等∵5c−且302a∴对于函数2yaxbxc=++，∵302a，

5c−，3当22x=−时，2111+2=-+222222yabcacac=+=+−−，当3x=时，1933=3yabcacac=++=+−−，当1x=时，3+=-yabcacac=+=−+，则321

yyy，故选：B．【点睛】本题考查二次函数的图象及性质；熟练掌握函数图象上点的特征是解题的关键．例2．（2020·全国九年级课时练习）二次函数f（x）的图象开口向上，D为顶点，与x轴交于A，B两点，与y轴交于点C，若三角形AB

C外接圆与y轴相切，且∠DAC＝150°，则x≠0时，()||fxx的最小值是_____．【答案】4323−【分析】设点A、B的坐标分别为（x1，0），（x2，0），抛物线的表达式为：y＝f（x）＝a（x﹣x1）（x﹣x2），△ABC外接

圆的圆心为P．求出点P、D的坐标，可得：AH2＝PH•HD，从而证明△AHP∽△DHA．再利用三角形相似角对应相等，进一步证明出△PAC为等边三角形，即得出x2＝3x1，a2x12＝13，即2113()()4xfxaxaxxx=+−，再利用完全平方式可知221111113343()424234

23xxaxaxaxaxaxaxxx+−−=−=−g，即可求解．【详解】4设点A、B的坐标分别为：（x1，0），（x2，0），设抛物线的表达式为：y＝f（x）＝a（x﹣x1）（x﹣x2），则点D的坐标为：212121()()22xxxxa−+−，，点C（0，ax1x2）

，设△ABC外接圆的圆心为P，圆P与y轴相切，连接CP，则CP⊥y轴，则点P的横坐标和点D的横坐标相同，其纵坐标和点C的纵坐标相同，故点P的坐标为：12121()2axxxx+，，∵PA＝PC，∴222121212()()()22xxxxaxx+−=+，∴a

2x1x2＝1，设函数对称轴交x轴于点H，连接AD，AH2＝（122xx+﹣x1）2＝（122xx−）2；PH•HD＝ax1x2•a（122xx−）2＝AH2，即AH2＝PH•HD，5而∠PHA＝∠DHA＝90°，故△AHP∽△DHA，∴∠APH＝∠HAD，∴∠PAD

＝∠PAH+∠DAH＝∠APH+∠PAH＝90°，故∠PAC＝∠CAD﹣∠PAD＝150°﹣90°＝60°，而PC＝PA，故△PAC为等边三角形，则∠OCA＝∠OCP﹣∠ACP＝90°﹣60°＝30°，在Rt△OCA中，OA＝12AC＝12PC，即12（x1+x2）＝2

x1，即x2＝3x1，而a2x1x2＝1，则a2x12＝13，则抛物线的表达式为：y＝f（x）＝a（x﹣x1）（x﹣3x1），故21111()(3)3()()4axxxxxfxaxaxxxx−−==+−，设：m、n为非负实数，由完全平

方公式得：2()20mnmnmn−=+−（当且仅当m＝n时等号成立），即m+n≥2mn，故2211111111()(3)33()43()42423423axxxxxxfxaxaxaxaxaxaxxxxx−−==+−−=−=−g，6故()fxx的

最小值为4323−，故答案为：4323−．【点睛】本题考查二次函数的综合运用、圆切线的性质、三角形相似的判定和性质、等边三角形的性质，综合性很强，题目难度很大．例3．（2021·江苏苏州市·九年级期末）直线33yx=−+与x轴交于点B，与y轴交于点C，

抛物线2yxbxc=−++经过B，C两点，与x轴的另一交点为A，连接AC，点P为AC上方的抛物线上一动点．（1）求抛物线的解析式；（2）如图①，连接BP，交线段AC于点D，若:5:16PDBD=，求此时点P的坐标；（3）如图②，连接PC．过点P作//PEy轴，交线段AC于点E

，若PCEV与ABCV相似，求出点P的横坐标及线段PE长．【答案】（1）223yxx=−−+；（2）1115,24P−，257,24P−；（3）32Px=−，194PE=或53Px=−，2209

PE=【分析】7（1）先根据直线与坐标轴的交点可求得B、C的坐标，再将B、C的坐标代入抛物线解析式列方程求解即可得出答案；（2）先求出A的坐标，利用待定系数法求出直线AC及BP的解析式，联立得出交点D的横坐标；如图过点P作PHx⊥轴于点H，作DGx⊥轴于点G，证明BDGBPH:△△，再根据相

似三角形的性质列方程求解即可得出答案；（3）设P点坐标为()2,23aaa−−+可得出点E的坐标，先求出PE、AC、EC的值，再分ABCEPC:△△，ABCECP:△△2种情况根据相似三角形的性质求得a的值，从而得出PE的值．

【详解】（1）直线33yx=−+与x轴交于点B，与y轴交于点C，令0x=，则3y=；令0y=，则1x=，B（1,0），C（0,3）Q抛物线2yxbxc=−++经过B，C两点，将B、C的坐标代入解析式可得103bcc−++=

=解得23bc=−=抛物线解析式为：223yxx=−−+；（2）令抛物线223=0yxx=−−+，可得1x=或3x=−A（-3,0）QC（0,3）8设直线AC的解析式为：1ykxb=+将A（-3,0），C（0,3）代入直线1ykxb=+，得11303k

bb−+==解得：113kb==直线AC的解析式为：3yx=+设P点坐标为（m,223mm−−+）设直线BP的解析式为：yaxn=+将B（1,0），P（m,223mm−−+）代入解析式yaxn=+中，得2023anamnmm+=+=−−+解得：33a

mnm=−−=+直线BP的解析式为：()33ymxm=−+++联立直线BP与直线AC()333ymxmyx=−+++=+解得4mxm=+如图过点P作PHx⊥轴于点H，作DGx⊥轴于点G9//DGPHQBDGBPH=，90BGDBHP==又DBGPBH=QBDGBPH

:△△QPD：BD=5:16BG：BH=16:21QBG=14BDmxxm−=−+，BH=1BPxxm−=−1164121mmm−+=−解得：12m=−或52m=−，经检验，12m=−，52m=−都是方程的根，当12m=−时

，215234mm−−+=；当52m=−时，27234mm−−+=故点P的坐标为（12−，154），（52−，74）；10（3）设P点坐标为()2,23aaa−−+(),3Eaa+()222333P

Eaaaaa=−−+−+=−−，22223332ACAOOC=+=+=,()2332ECaa=−−=−,//PEyQ轴PECACO=又3OAOAOCOA==⊥Q，,45CABACO==PECCAB=①当ABCEPC:△△时ACABECEP=即23242332aaaa

=−−+−−−解得：53a=−或0a=经检验0a=不是方程的根，应舍去，22039PEaa=−−=；②当ABCECP:△△时ABACECEP=即24322332aaaa=−−+−−−11解得：32a=−

或0a=经检验0a=不是方程的根，应舍去，2934PEaa=−−=．【点睛】本题考查了二次函数的综合、相似三角形的判定及性质、一次函数的解析式，解题的关键是熟练运用待定系数法求解析式，并运用相似三角形的判定及性

质得出边角关系，分类讨论．【好题演练】一、单选题1．（2020·台州市路桥区桐屿镇中学九年级月考）我们定义一种新函数：形如2yaxbxc++＝（a≠0，b2﹣4ac＞0）的函数叫做“鹊桥”函数．小丽同学画出了“鹊桥”函数y＝

|x2﹣2x﹣3|的图象（如图所示），并写出下列五个结论：其中正确结论的个数是（）①图象与坐标轴的交点为（﹣1，0），（3，0）和（0，3）；②图象具有对称性，对称轴是直线x＝1；③当﹣1≤x≤1或x≥3时，函数值y随x值的增大而增大；④当x＝﹣1或x＝3时，函数的最小

值是0；⑤当x＝1时，函数的最大值是4，12A．4B．3C．2D．1【答案】A【分析】由（-1,0），（3,0）和（0,3）坐标都满足函数223yxx=−−，∴①是正确的；从图象可以看出图象具有对称性，对称轴可用对称轴公式求得是直线1x=，②也是正确的；根据函数的图象和性质，发现当11

x−或3x时，函数值y随x值的增大而增大，因此③也是正确的；函数图象的最低点就是与x轴的两个交点，根据0y=，求出相应的的值为1x=−或3x=，因此④也是正确的；从图象上看，存在函数值大于当1x=时的223=4yxx=−−，因此⑤时不正确的；逐个判断之后，

可得出答案．【详解】解：①∵（-1,0），（3,0）和（0,3）坐标都满足函数223yxx=−−，∴①是正确的；②从图象可知图象具有对称性，对称轴可用对称轴公式求得是直线1x=，因此②也是正确的；③根据函数的图象和性质，发现当11x−或3x时，

函数值y随x值的增大而增大，因此③也是正确的；④函数图象的最低点就是与x轴的两个交点，根据y＝0，求出相应的x的值为1x=−或3x=，因此④也是正确的；13⑤从图象上看，存在函数值要大于当1x=时的223=4yxx=−−，因此⑤是不正确的；故选A【点睛】理解“鹊桥”函数

2yaxbxc++＝的意义，掌握“鹊桥”函数与2yaxbxc++＝与二次函数2yaxbxc++＝之间的关系；两个函数性质之间的联系和区别是解决问题的关键；二次函数2yaxbxc++＝与x轴的交点、对称性、对称轴及最值的求

法以及增减性应熟练掌握．2．（2020·广西南宁市·三美学校九年级学业考试）如图是抛物线()20yaxbxca=++，其顶点为()1,n，且与x轴的个交点在点()3,0和()4,0之间，则下列结论正确的个数是（）个①若抛物线与x轴的另一个交点为(),0k，则21k−

−；②can−=；③若xm−时，y随x的增大而增大，则1m−．A．0B．1C．2D．314【答案】D【分析】①根据抛物线的对称性得：AD=BD，列不等式结论；②将顶点坐标（1，n）代入抛物线的解析式中，列两式可得结论；③根据抛物线的对称轴由此作判断；【详解】解：①如图，设抛物线与x轴的

交点为A和B（A在B的右侧），则3-1＜AD＜4-1，2＜AD＜3，由对称性得：AD=BD，∴2＜BD＜3，∵B（k，0），∴BD=1-k，∴2＜1-k＜3，∴-2＜k＜-1，所以选项①正确；②∵抛物线的顶点坐标为（1，n），∴1

2ba−=，b=-2a，a+b+c=n，a-2a+c=n，15∴-a+c=n，c-a=n，所以选项②正确；③∵抛物线的对称轴是直线x=1，∴若x＜1时，y随x的增大而增大，则m≥-1；所以选项③正确；故选D

【点睛】本题考查了二次函数图象与系数的关系：对于二次函数y=ax2+bx+c（a≠0），明确以下几点：①二次项系数a决定抛物线的开口方向和大小：当a＞0时，抛物线向上开口；当a＜0时，抛物线向下开口；②一次项系数b和二次项系数a共同决定对称轴的位置：当a与b同号时（即ab＞

0），对称轴在y轴左；当a与b异号时（即ab＜0），对称轴在y轴右；③常数项c决定抛物线与y轴交点位置：抛物线与y轴交于（0，c）．二、填空题3．（2020·浙江杭州市·九年级期末）如图，抛物线y＝﹣x2+2x+m+1（m为常数）交y轴于点A，与x轴的一个交点在2和3之间，顶点为B．①抛物线y＝﹣

x2+2x+m+1与直线y＝m+2有且只有一个交点；②若点M（﹣2，y1）、点N（12，y2）、点P（2，y3）在该函数图象上，则y1＜y2＜y3；③将该抛物线向左平移2个单位，再向下平移2个单位，所得抛物线解析式为y＝﹣（x+1）2+m；④点A关于直线x＝1的对

称点为C，点D、E分别在x轴和y轴上，当m＝1时，四边形BCDE周长的最小值为342+．16其中正确判断的序号是_____．【答案】①③④【分析】联立两个函数解析式，消去y，可得2210xx−+=，由方程有两个相等的实数根，从而可判断①，由抛物线

的对称轴为：1x=，可得：点P（2，y3）关于x＝1的对称点为()30,Py，再利用抛物线的开口向下，当x＜1时，y随x增大而增大，从而可判断②，由抛物线的平移规律：左加右减，上加下减，可判断③，当m＝1时，抛物线的解析式为：y＝﹣x2+2x+2，作点B关于

y轴的对称点()13B−，，作C点关于x轴的对称点()22C−，，从而可得四边形BCDE周长的最小值为BCBC+，由此即可得答案．【详解】解：①把y＝m+2代入y＝﹣x2+2x+m+1中，得x2﹣2x+1＝0，

∵△＝4﹣4＝0，∴此方程两个相等的实数根，则抛物线y＝﹣x2+2x+m+1与直线y＝m+2有且只有一个交点，故①正确；②∵抛物线的对称轴为x＝1，∴点P（2，y3）关于x＝1的对称点为()30,Py，∵a＝﹣1＜

0，17∴当x＜1时，y随x增大而增大，又∵﹣2＜012＜，且点M（﹣2，y1）、点N（12，y2）、点()30,Py在该函数图象上，∴y2＞y3＞y1，故②错误；③将该抛物线向左平移2个单位，再向下平移2个单位所

得抛物线的解析式为：()()222212yxxm=−+++++−，即y＝﹣（x+1）2+m，故③正确；④当m＝1时，抛物线的解析式为y＝﹣x2+2x+2，∴A（0，2），C（2，2），B（1，3），作点B关于y轴的对称点()13B−，，作C点关于x轴的对称点()22C−，，连接BC

，与x轴、y轴分别交于D、E点，,BBCC相交于M，如图所示：则BEEDCDBCBEEDCDBCBCBC+++=+++=+，根据两点之间线段最短，知BC最短，而BC的长度一定，∴此时，四边形BCDE周长的最小

值为BCBC+，18即22222222B'MC'MBMCM3511342+++=+++=+，故④正确；故答案为：①③④．【点睛】本题考查的是二次函数与直线的交点问题，二次函数的性质，二次函数图象的平移，利用二次函数的对称性求解周长的最小值，掌握以上知识是解题的关键．4．（20

20·温州市第十二中学九年级期中）如图，抛物线()()13yaxx=+−与x轴交于A，B两点（点A在B的左侧），点C为抛物线上任意一点．．．．（不与A，B重合），BD为ABCV的AC边上的高线，抛物线顶点E与点D的

最小距离为1，则抛物线解析式为______．【答案】2339424yxx=−−【分析】根据题意可确定出A，B两点的坐标，从而求出对称轴为x=1，依题意要使DE最小则D点必在对称轴上，从而根据题意画出图形求解即可．【详解】解：如图所示，使DE最小则D点必在对

称轴x=1上，过点E作EF⊥AB，则AF=BF，19∴AD=BD，∵BD为ABCV的AC边上的高线，∴∠ADB=90°，∴∠DBF=∠BDF=45°，∴DF=BF=2．当x=1时，y=-4a，∵抛物线开口向上，∴a>0，∴EF=4a．∵DE=1，∴4a-2=1解得

：a=34．∴抛物线解析式为3(1)(3)4yxx=+−即2339424yxx=−−故答案为：2339424yxx=−−．【点睛】20本题考查了二次函数的综合题，结图象求最值问题，利用好数形结合找出最小值的点是解题

的关键．三、解答题5．（2021·广西柳州市·九年级期末）二次函数23yaxbx=++的图象与x轴交于(2,0)A，(6,0)B两点，与y轴交于点C，顶点为E．（1）求这个二次函数的表达式，并写出点E的坐标；（2）如图，D是该二次函数图象的

对称轴上一个动点，当BD的垂直平分线恰好经过点C时，求点D的坐标．【答案】（1）21234yxx=−+，(4,1)E−；（2）D的坐标为(4,329)+或(4,329)−【分析】（1）根据待定系数法即可得出抛物线的解析式，由配方法求出E点坐标即可；（2）

先求出点D的坐标，连接CB，CD，由点C在线段BD的垂直平分线CN上，得CBCD=．设D（4，m），由勾股定理可得22224(3)63m+−=+，解方程即可得出答案．【详解】解：（1）将(2,0)A，(6,0)B代入23yaxbx=++，21得423036630a

bab++=++=，解得142ab==−二次函数的解析式为21234yxx=−+．221123(4)144yxxx=−+=−−Q，(4,1)E−．（2）当0x=时，3y=，(0,3)C连接CB，CD，由点C在线段BD的垂

直平分线CN上，得CBCD=．设D（4，m），(0,3)CQ，由勾股定理可得：22224(3)63m+−=+．解得329m=．满足条件的点D的坐标为(4,329)+或(4,329)−．22图1图2【点睛】本题考查了二次函数综合题、考查了待定系数法、二

次函数的图象及性质、垂直平分线的性质、勾股定理，熟练掌握二次函数的性质是解题的关键．6．（2020·淮南市龙湖中学九年级月考）探究函数y=x|x-2|的图象与性质．小娜根据学习函数的经验，对函数y=x|x-2|的图象与性质进行

了探究．下面是小娜的探究过程，请补充完整：（1）下表是x与y的几组对应值．请直接写出：m=，n=；（2）如图，小娜在平面直角坐标系xOy中，描出了上表中已经给出的各组对应值为坐标的点，请再描出剩下的两个点，并画出该函数的图象；（3）结合画出的

函数图象，解决问题：若方程x|x-2|=a有三个不同的解，记为x1，x2，x3，且x1＜x2＜x3．请直接写出x1+x2+x3的取值范围．23【答案】（1）m=1，n=0；（2）见详解；（3）4<x1+x2+

x3<3+2．【分析】（1）把x1=和x2=代入y=x|x-2|，即可求得m、n的值；（2）画出该函数图象即可；（3）根据题意可知1202xx，且101x，212x，令21,2xxx−=时，求解x的值，即

可得出3x的范围；再结合1x与2x关于1x=对称，得出12121,22xxxx+=+=，进一步即可得出结果．【详解】解：（1）把x1=代入y=x|x-2|，得m111==把x2=代入y=x|x-2|，得n200=

=故答案为：m=1，n=0；（2）如图：24（3）Q2xxa−=有三个解为1x，2x，3x，且123xxx，则2yxx=−与ya=图象有三个交点，1202xx，且101x，212x，令21,2xxx−=时，解得21x

=+3221x+12,xxQ关于1x=对称，12121,22xxxx+=+=123423xxx+++．【点睛】此题主要考查二次函数的图象和性质，二次函数图象上点的坐标特征，利用了数形结合

思想，正确画出函数图象是解题关键．25