【文档说明】5.3.1 函数的单调性-2022-2023学年高二数学《考点•题型 •技巧》精讲与精练高分突破系列（人教A版2019选择性必修第二册）.docx，共(27)页，2.293 MB，由envi的店铺上传

转载请保留链接：https://www.doc5u.com/view-828aeafe46e46048be1ea81c97686829.html

以下为本文档部分文字说明：

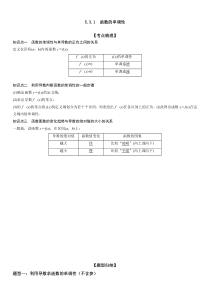
5.3.1函数的单调性【考点梳理】知识点一函数的单调性与其导数的正负之间的关系定义在区间(a，b)内的函数y＝f(x)：f′(x)的正负f(x)的单调性f′(x)>0单调递增f′(x)<0单调递减知识点二利用导数判断函数的单调性的一般步骤(1)确定函数y＝f(x)的定义域；(2)求出导数f′(

x)的零点；(3)用f′(x)的零点将f(x)的定义域划分为若干个区间，列表给出f′(x)在各区间上的正负，由此得出函数y＝f(x)在定义域内的单调性．知识点三函数图象的变化趋势与导数的绝对值的大小的关系一般地，设函数y＝f(x)，在区间(a，b)上：导数的绝对值函数值变化函

数的图象越大快比较“陡峭”(向上或向下)越小慢比较“平缓”(向上或向下)【题型归纳】题型一：利用导数求函数的单调性（不含参）1．（2022·全国·高二）函数21ln2yxx=−的单调递减区间为（）A．()1,1−B．()0,1C．)1

,+D．()0,+2．（2022春·福建莆田·高二莆田一中校考期中）若函数222()exxxfx++=，则()fx的一个单调递增区间是（）A．1,2−B．1,12C．1,12−D．1,2−

−3．（2021秋·宁夏中卫·高二海原县第一中学校考期中）已知函数32()2fxxxx=−−+.(1)求曲线()fx在点()()22f,处的切线方程；(2)求()fx的单调区间.题型二：由函数的单调性求参数4．（2022·高二课时练习）若函数()2lnfxxaxx=−+在区间()1,e

上单调递增，则实数a的取值范围是（）A．)3,+B．(,3−C．23,e1+D．(2,e1−+5．（2022秋·四川成都·高二校考期中）已知函数()321fxxxax=+−+在R上为单调递增函数，则实数a的取值范围为（）

A．1,3−−B．1,3−−C．1,3−+D．1,3−+6．（2022秋·天津和平·高二天津一中校考期中）已知函数()()()3223110fxmxmxmm=+−−+的单调递减区间是()0

,4，则m=（）A．3B．13C．2D．12题型三：由函数在区间的单调性求参数7．（2018春·湖南邵阳·高二统考期末）设函数()3212132afxxxx=−++，若()fx在区间()2,1−−内存在单调递减区间，则实数a

的取值范围是（）A．()22,+B．)22,+C．(,22−−D．(),22−−8．（2022秋·黑龙江哈尔滨·高二哈尔滨市阿城区第一中学校校联考期末）已知函数()()24exfxxxa=−+在区间2,3−上单调递减，则实数a的取值范

围是（）A．(,4−−B．(,5−C．(,1−D．(,8−−9．（2022秋·安徽·高二校联考期末）若函数()lnafxxx=+在2,4上为增函数，则a的取值范围为（）A．(,2−B．)2,+C．(,4−D．)4,+题型四：函数与导函数图像

的关系10．（2022秋·四川绵阳·高二校考期中）已知函数()yxfx=（()fx是函数()fx的导函数）的图象如图所示，则()yfx=的大致图象可能是（）A．B．C．D．11．（2022秋·浙江宁波·高二宁波市李惠利中学校联考期中）

函数()yfx=在定义域3,32−内可导，图像如图所示，记()yfx=的导函数为()yfx=，则不等式()0fx的解集为（）A．)1,12,33−B．1481,,233−C．31,1,223−−D．3148

,,2333−−12．（2022秋·北京·高二北京四中校考期中）已知函数()fx与()fx的图象如图所示，则函数()exfxy=（）A．在区间()2,0−上是减函数B．在区间()13,xx上是

减函数C．在区间()35,xx上是减函数D．在区间()24,xx上是减函数题型五：含参分类讨论函数的单调性13．（2022·高二课时练习）求函数()()32123fxxaxa=−+R的单调区间.14．（2022秋·重庆璧山·高二重庆市璧山来凤

中学）已知函数221()2ln()2fxaxxaxa=−++R.(1)当1a=时，求曲线()yfx=在(1,(1))f处的切线方程；(2)讨论函数()fx的单调性；15．（2022秋·内蒙古呼伦贝尔·高二校考期末）已知函数()2(n2)lafxaxxx−+=+（aR）

.(1)2a=−，求函数()fx在()()1,1f处的切线方程；(2)讨论函数()fx的单调性.【双基达标】一、单选题16．（2022·全国·高二假期作业）已知2()ln1fxxxmx=++−在区间(1,2)上为单调递增函数，则实数m的取值范围是（）A．4m−B．4m−C．

3m−D．3m−17．（2022春·江西宜春·高二上高二中校考阶段练习）若函数()21()ln12gxxxbx=+−−存在单调递减区间，则实数b的取值范围是（）A．)3,+B．()3,+C．(),3−D．(,3−18．（2022秋·江西赣

州·高二江西省信丰中学校考阶段练习）若定义在R上的函数()fx的导函数()fx为，且满足()()fxfx，则(2017)f与e(2016)f的大小关系为（）A．(2017)f＜e(2016)fB．(2017)f=e(2016)fC．(2017)f＞e(2016

)fD．不能确定19．（2022·高二课时练习）已知函数()yfx=在定义域3,32−内可导，其图象如图所示.记()yfx=的导函数为()yfx=，则不等式()0xfx的解集为（）A．)31,0,12,323−−B．18,01,2,33

3−C．)1,12,33−D．31148,,,323233−−20．（2022·高二）若函数2()(1)exfxxax=−+在(1,0)−上单调递减，则实数a的取值范围是（）A．(,3−B．)3,+C．

)1,+D．(,1−21．（2022春·陕西延安·高二）已知函数()()21ln2fxxxmxxm=−−R．(1)若0m=，求函数()fx的单调区间；(2)若函数()fx在()0,+上是减函数，求实数m的取值范围．22．（2022秋·河南郑州·高二

统考期末）已知函数()()221lnafxxaxx=−+−.(1)当1a=时，求该函数在点11,22f处的切线方程；(2)讨论函数()fx的单调性.【高分突破】一、单选题23．（2022·高二）已知函数()()321233fxx

bxbx=++++在R上单调递增，则实数b的取值范围是（）A．()1,2-B．1,2−C．()(),12,−−+D．(),22,−−+U24．（2021秋·宁夏中卫·高二海原县第一中学校考期中）已知函数()fx的导函数是()fx，且()()10xfx+

，则（）A．()()01ffB．()()12ffC．()()12ff−D．()()32ff−−25．（2022秋·贵州贵阳·高二校联考期末）设1.01ea=，3eb=，ln3c=，则a，b，c的大小关系是（）A．bac

B．cabC．acbD．abc26．（2022秋·辽宁丹东·高二统考期末）若函数()fx在R上可导，且满足()()0fxxfx−，则（）A．()()2332ffB．()()2332ffC．()()3322

ffD．()()3322ff27．（2022秋·广东清远·高二统考期末）已知函数()ln2fxaxx=+在)1,+上单调递增，则实数a的最小值为（）A．2−B．2C．1−D．1二、多选题28．（2022秋·广东潮州·高二饶平县第二中学校考开学考试）已知函数()ln(1

)fxxx=+，则（）A．()fx在(0,)+单调递增B．()fx有两个零点C．曲线()yfx=在点11,22f−−处切线的斜率为1ln2−−D．()fx是奇函数29．（2022·高二课时练习）已知函数()fx

的定义域为R，其导函数()fx的图象如图所示，则对于任意12,xxR（12xx），下列结论正确的是（）A．()()()12120xxfxfx−−B．()()()12120xxfxfx−−C．()()121222fxfxxxf++D．()()121222

fxfxxxf++30．（2022·高二单元测试）已知函数()lnfxxx=，若120xx，则下列结论正确的是（）A．()()2112xfxxfxB．()()1122xfxxfx++C．()()1212fxfxxx−−D．当ln1x−时，()()()112

2212xfxxfxxfx+31．（2022秋·辽宁沈阳·高二沈阳二中校考期末）已知函数()fx的定义域为R，且()1fx，()34f=，则下列结论中正确的有（）A．()fx为增函数B．()()gxfxx=−为增函数C．()2

14fx−的解集为(),2−D．()212fxx−的解集为()2,+32．（2022秋·广东潮州·高二统考期末）已知函数()fx与()fx的图象如图所示，则下列结论正确的为（）A．曲线m是()fx的图象，曲线

n是()fx的图象B．曲线m是()fx的图象，曲线n是()fx的图象C．不等式组()()02fxfxx的解集为()0,1D．不等式组()()02fxfxx的解集为41,33

3．（2022秋·广东云浮·高二统考期末）已知定义在R上的函数()fx的导函数为()fx，且xR，()()210fxfx+，则下列结论正确的有（）A．若ab，则()()()()10fafbfafb−++B．若ab，则()()()()10fafb

fafb−++C．若()fx是增函数，则()2fx是减函数D．若()fx是减函数，则()2fx是增函数三、填空题34．（2022秋·四川绵阳·高二校考期末）已知定义在R上的函数()fx的导函数为()fx，且满足()()0fxfx−，则不等式()()42e3

4exfxfx−的解集为__________.35．（2022·全国·高二专题练习）设()fx是定义在R上的奇函数，且(2)0f=，当0x时，有2()()0xfxfxx−恒成立，则不等式2()0xfx≤的解集为__．36．（20

22秋·上海杨浦·高二上海市杨浦高级中学校考期末）若函数()lnfxaxx=−在()1,x+是严格增函数，则实数a的最小值是_________.37．（2022·全国·高二）已知函数()3211232gxxa

xx=−+，若()gx在()2,1−−内为减函数，则实数a的取值范围是______．38．（2022·高二单元）已知函数()eecosxxfxx−=++，则不等式(2)(2)fmfm−的解集为__________．39．（2022·高二）已知函数

()2lnxaxfxx=++的单调递减区间为1,12，则a的值为________．四、解答题40．（2022秋·陕西渭南·高二统考期末）函数()()2exfxxaxb=++，若曲线()yfx=在点()()0,0f处的切线方程为：450xy++=.(1)求,ab的值；(2

)求函数()fx的单调区间.41．（2022秋·上海浦东新·高二上海市进才中学期末）已知函数2()lnfxaxx=+.(1)当2a=−时，求函数()fx的单调区间；(2)若2()()xgfxx=+在[1,)+上为严格增函数，求实数a的取值范围.42．（2022秋·黑龙江哈尔

滨·高二哈尔滨三中）已知函数2()(32)34exfxaxaxa=−+++，aR．(1)当1a=时，求函数()fx在点()1,(1)f处的切线方程；(2)讨论函数()fx的单调性．43．（2022秋·新疆阿克苏·高二校考期末）已知函数()()212lnR2fxxaxxa=−

−.(1)当1a=时，求函数()fx的单调区间和极值；(2)若函数()fx在区间)1,+上单调递增，求实数a的取值范围.44．（2022秋·河南郑州·高二统考阶段练习）已知函数()()21ln112fxxaxax=−+−+．

(1)当2a=时，求曲线()yfx=在1x=处的切线方程：(2)讨论()fx的单调性．参考答案：1．B【分析】求出导函数，令导函数小于0，即可得到单调递减区间.【详解】解：由题意，0x在21ln2yxx=−中，211xyxxx−=−=当0y=时

，解得=1x−（舍）或1x=当0y即01x时，函数单调递减∴单调递减区间为()0,1故选：B.2．B【分析】对函数进行求导，令()0fx即可求解【详解】由222()exxxfx++=可得(

)()()()()2241e22e21()1eexxxxxxxxfxx+++−+=−−=，令()0fx，解得112x，所以()fx的单调递增区间是1,12，故选：B3．(1)7100xy−−=(2)递增区间为1(,)3−−，(1,)+；递

减区间为1,13−【分析】（1）求出函数的导函数，再求得()27f=与()24f=，利用点斜式可求得曲线()fx在点()()22f,处的切线方程；（2）由()()()2321131fxxxxx=−−=−+，利用导函数

()fx与函数()fx的单调性的关系可得答案.【详解】（1）()322fxxxx=−−+，()()()2321131fxxxxx=−−=−+，()27f=，又()24f=，曲线()fx在点()()22

f,处的切线方程为()472yx−=−，即7100xy−−=；（2）()()()2321131fxxxxx=−−=−+，∴当()1,1,3x−−+时，()0fx，当1,13x−时，()0fx，()fx在1(,)3

−−，(1,)+上单调递增，在1,13−上单调递减.()fx的递增区间为1(,)3−−，(1,)+；递减区间为1,13−.4．B【分析】根据函数的单调性与导函数之间的关系，将单调性转化为导函数恒大于或等于0，即可求解.【详解】依题意()120fxxax=−

+在区间()1,e上恒成立，即12axx+在区间()1,e上恒成立.令()()121egxxxx=+，则()22212120xgxxx−=−=，所以()gx在()1,e上单调递增，则()3gx，所以3a.故选:B.5．A【分析】由题设可得

()0fx¢³在R上恒成立，结合判别式的符号可求实数a的取值范围.【详解】()232fxxxa=+−，因为()fx在R上为单调递增函数，故()0fx¢³在R上恒成立，所以4120a=+即13a−，故选：A.6．B【分析】利用导数结合韦达定理得出m的值.【详解】函数()

()()3223110fxmxmxmm=+−−+，则导数()()2361fxmxmx=+−令()0fx，即()23610mxmx+−，∵0m，()fx的单调递减区间是()0,4，∴0，4是方程()236

10mxmx+−=的两根，∴()2104mm−+=，040=，∴13m=故选：B.7．D【分析】根据函数单调性与导数的关系可知，()0fx在()2,1−−内存在解，即可解出．【详解】由题可知，()0fx在()2,1−−内存在解，因为()22fxxax=−+，所以()0fx在

()2,1−−内存在解，等价于2xax+在()2,1−−内存在解，易知函数2yxx=+在()2,2−−上递增，在()2,1−−上递减，所以max222xx+=−，当且仅当2x=−时取得，所以22a−．故选：D．8

．A【分析】首先求函数的导数，根据题意转化为2240xxa−+−在2,3−上恒成立，即()2min24axx−++，即可求实数a的取值范围.【详解】因为函数()()24exfxxxa=−+在2,3−上单调递减，所以()()224e0xfxxxa−+−=在2

,3−上恒成立，则2240xxa−+−在2,3−上恒成立，即()2min24axx−++，又()222415xxx−++=−−+，当2x=−时，224xx−++的最小值为4−，故4a−．故选：A9．A【分析】根据在2,

4上()0fx恒成立求解即可【详解】()221axafxxxx−=−=，因为函数()lnafxxx=+在[2，4]上为增函数，所以()0fx在2,4上恒成立，故0xa−在2,4上恒成立，故ax在2,4上恒成立，所以2

a.故选：A10．C【分析】设函数()yxfx=的图象在x轴上最左边的一个零点为a，根据函数的图象得到()fx的正负，即得解.【详解】解：设函数()yxfx=的图象在x轴上最左边的一个零点为a，且21a−−.当2x

a−时，()0,()0,()yxfxfxfx=在(2,)a−上单调递增；当0ax时，()0,()0,()yxfxfxfx=在(,0)a上单调递减.故选：C11．C【分析】()0fx的解集即为()yfx=单调递增区

间，结合图像理解判断．【详解】()0fx的解集即为()yfx=单调递增区间结合图像可得()yfx=单调递增区间为31,,1,223−−则()0fx的解集为31,1,223−−故选：C．12．B【分析】求

导可得()()exfxfxy−=；分别判断y在各个区间内的正负，由此可得结果.【详解】由()exfxy=得：()()()()2eeeexxxxfxfxfxfxy−−==，对于A，当()12,xx−时，()()fxfx，即0y，()exfxy=在()12,

x−上是增函数，A错误；对于B，当()13,xxx时，()()fxfx，即0y，()exfxy=在()13,xx上是减函数，B正确；对于C，当()35,xxx时，()()fxfx，即0y，()exfxy=在()35,xx上是增函数，C错误；对于

D，当()34,xxx时，()()fxfx，即0y，()exfxy=在()34,xx上是增函数，D错误.故选：B.13．见解析【分析】求导分a与0的大小关系分别讨论导函数的正负区间与原函数的单调性即可.【详解】因为()

32123fxxax=−+，所以()22fxxax=−.由()220fxxax=−=，解得x＝0或x＝2a.当a＝0时，()20fxx=，所以f（x）在R上严格增，单调增区间为(),−+；当0a时，当()(),02,xa−+时，()0fx¢>；

当()0,2xa时，()0fx，所以f（x）的单调增区间为(),0−及()2,a+，单调减区间为（0，2a）；当a<0时，当()(),20,xa−+时，()0fx¢>；当()2,0xa时，()0fx，所以f（x）的单调增区间为(),2a−及()0,+，单调减区间为

（2a，0）.14．(1)32y=(2)单调性见解析【分析】（1）先求解(1)f的值，再求解(1)f的值，利用导数的几何意义即可求解.（2）分类讨论a的取值范围，利用导数求解函数()fx的单调性.（1）解：当1a=

时，21()2ln2fxxxx=−++，222()1(0)xxfxxxxx+−=−++=，∴()01f=，又3(1)2f=，∴曲线()yfx=在(1,(1))f处的切线方程为32y=；（2）解：因为22222()(2)()(0)axax

axaxafxxaxxxx−+−−+++===.当0a=时，()0,()fxxfx=在(0,)+上为增函数；当a<0时，当(0,2)xa−时，()0fx，当(2,)xa−+时，()0fx，∴()fx在区间(

0,2)a−上单调递减，在区间(2,)a−+上单调递增；当0a时，当(0,)xa时，()0fx，当(,)xa+时，有()0fx，∴()fx在区间(0,)a上单调递减，在区间(,)a+上单调递增.15．(1)10y−=(2)答案见解析【

分析】（1）代入2a=−，求导得切线的斜率()1kf=，进而求得切线方程；（2）先求导，再分0a，02a，2a=和2a讨论导数的正负，进而求得函数的单调性.（1）2a=−时，()22lnfxxx=−，()22fxxx=−，

切线的斜率()10,(1)1kff===，则切线方程为10y−=；（2）函数()fx的定义域为()0,+，且()()()1(2)22xaxxafxaxx−−−++==，①当0a时，20xa−，由()0fx¢>，得1x；由()

0fx，得01.x则函数()fx的单调递增区间为()1,+，单调递减区间为()0,1.②当012a，即02a时，由()0fx¢>，得02ax或1x；由()0fx，得12ax.则函数

()fx的单调递增区间为0,2a，()1,+，函数()fx的单调递减区间为,12a.③当12a=，即2a=时，()0fx恒成立，则函数()fx的单调递增区间为()0,+.④当12a，即2a时，由()0

fx¢>，得01x或2ax；由()0fx，得12ax，则函数()fx的单调递增区间为()0,1，,2a+，函数()fx的单调递减区间为1,2a.综上所述，当0a时，函数()fx在()1,+上单调递增，在()0,1上单调递减；当02a时，

函数()fx在0,2a和()1,+上单调递增，在,12a上单调递减；当2a=时，函数()fx在()0,+上单调递增；当2a时，函数()fx在()0,1和,2a+上单调递增，在1,2a上单调递减.16．D【分析】求出导函数，推出

12mxx−+在区间(1,2)上恒成立，构造函数，求解函数的最值，从而求出实数m的取值范围．【详解】2()ln1fxxxmx=++−在区间(1,2)上为单调递增函数则1()20fxxmx=++在区间(1,2)上恒成立即12mxx−+在区间(1,2)上恒成立设1(

)2hxxx=−+，(1,2)x22221))()2012(12(12xxxhxxxx=−+=−+=−函数()hx在(1,2)上是减函数，则()(1)3hxh=−所以3m−．故选：D．17．B【分析】首先计算出()'gx,由()gx存在单调递减区间知(

)'0gx<在()0,+上有解即可得出结果.【详解】函数()21()ln12gxxxbx=+−−的定义域为()0,+，且其导数为()'1(1)gxxbx=+−−．由()gx存在单调递减区间知()'0gx<在()0,+上有解，即1(1)xbx+−−有解．因为函数()gx的定义域为()0,+

，所以12xx+．要使1(1)xbx+−−有解，只需要1xx+的最小值小于1b−，所以21b−，即3b，所以实数b的取值范围是()3,+．故选:B．18．C【分析】根据题中的不等关系构造新函数，对新函数求导，根据

不等关系得到新函数的单调性，进而赋值得到结论.【详解】设()()xfxgx=e，则有()()()exfxfxgx−=，又因为()()fxfx，所以()()()0exfxfxgx−=在R上恒成立，则函数

()()xfxgx=e在R上单调递增，则()()20172016gg，即()()2017201620172016eeff，即(2017)f＞e(2016)f.故选：C.19．A【分析】根据原函数图象与导函数的关系，即可得到结果.【详解】对

于不等式对()0xfx，当302x−时，()0fx，则结合图象，知原不等式的解集为31,23−−；当03x时，()0fx，则结合图象，知原不等式的解集为)0,12,3．综上，原不等式的解集为31,[0,1][2,3)23−−

．故选：A20．C【分析】根据函数的区间单调性，利用导数有1ax+在(1,0)−上恒成立，即可得参数范围.【详解】由2()(1)exfxxax=−+，得2()e(2)1[]e(1)(1)xxfxxaxaxax=+−+−=+−+.由于函数()()21ex

fxxax=−+在(1,0)−上单调递减，所以()0fx在(1,0)−上恒成立，则1ax+在(1,0)−上恒成立，所以1a.故选：C21．(1)单调递减区间是()0,1，单调递增区间是()1,+，(2)1em【分析】

(1)先对函数()fx求导，利用导数判断函数的单调区间；(2)已知函数()fx在()0,+上是减函数，可知知()0fx恒成立，利用参数分离法,求lnxx的最大值即可求解.【详解】（1）当0m=时，()l

n,(0,)fxxxxx=−+，()ln,()0,1.fxxfxx===()001fxx，()01fxx所以()fx的单调递减区间是()0,1，单调递增区间是()1,+（2）由函数()f

x在()0,+上是减函数，知()0fx恒成立，()()21lnln2fxxxmxxfxxmx=−−=−．由()0fx恒成立可知ln0xmx−恒成立，则maxlnxmx≥，设()lnxxx=，则()21lnxxx−

=，由()()00,exx，()<0exx知，函数()x在()0,e上递增，在()e,+上递减，∴()()max1eex==，∴1em．22．(1)353ln20xy−−+=(2)答案见解析【分析

】（1）求出导函数，计算导数1()2f得切线斜率，再求出1()2f，由点斜式得切线方程并化简；（2）求出导函数()fx，然后分类讨论确定()0fx和()0fx的解可得单调性．(1)当1a=时，2()3lnfxxxx=−−，该函数定

义域为()0,+，则22223232(1)(2)()1xxxxfxxxxx−+−−=−+==.所以116832f=−+=.又11173ln43ln22222f=−−=−+，所以116

832f=−+=.所以该函数在点11,22f处的切线方程为713ln2322yx−−+=−，即353ln20xy−−+=.(2)由题可得2222212(21)2(2)(1)()1aaxaxaxaxfxxxxx+−

++−−=−+==，令()0fx=，得1x=或2xa=.而该函数定义域为(0,)+，则①若0a，则20xa−，在区间（0，1）上，()0fx；在区间()1,+上，()0fx¢>，故函数()fx在（0，1）上单调递减，在()1,+上

单调递增；②若102a，即021a，则在区间()0,2a和(1,)+上，()0fx¢>；在区间()2,1a上，()0fx，故函数()fx在()0,2a和()1,+上单调递增，在()2,1

a上单调递减；③若12a=，即21a=，则在区间(0,)+上，()0fx恒成立，且仅在1x=处取得等号，故函数()fx在(0,)+上单调递增；④若12a，即21a，则在区间（0，1）和(2,)a+上，()0fx¢>；在区间()1,2a上，()0fx，故函数()

fx在（0，1）和(2,)a+上单调递增，在()1,2a上单调递.23．B【分析】()fx在R上单调递增()0fx在R上恒成立，()fx为二次函数，结合列不等式求解即可【详解】由题意得()222fxbxbx+++=，∵()fx在R上单调递增，∴2220xbxb+++

在R上恒成立，∴0，即220bb−−，解得12b−．故选：B24．D【分析】对于ABD，通过对10x+与10x+的讨论，得到()fx的单调性，从而即可判断；对于C，举反例即可排除.【详解】对于AB，()(

)10xfx+，当10x+，即1x−时，()0fx，()fx在(1,)−+上单调递减；()(0)1ff，()()12ff，故AB错误；对于D，当10x+，即1x−时，()0fx，()fx在(,1)−−上单调递增；()()32ff−−，故D正确；对于C，令()(

)21fxx=−+，满足()fx在(1,)−+上单调递减，在(,1)−−上单调递增，此时()()1092ff−=−=，故C错误.故选：D.25．D【分析】分析可得2a，(1,2)b，(1,2)c，令()ln,[e,)exfxxx=−+

，利用导数可得()fx的单调性，根据函数单调性，可比较ln3和3e的大小，即可得答案.【详解】由题意得1.011ee2a=，3(2e1,)b=，ln3(1,2)c=，令()ln,[e,)exfxxx=−+，则11e()0eexfxxx−=−=，所以

()fx在[e,)+为减函数，所以(3)(e)ff，即3eln3lne0ee−−=，所以3ln3e，则1.013eln3e，即abc.故选：D26．A【分析】构造函数()()(0)fxgxxx=，根据函数()fx在R上可导，且满足()()0

fxxfx−，利用导数研究其单调性即可得出．【详解】构造函数()()(0)fxgxxx=，函数()fx在R上可导，且满足()()0fxxfx−，2()()()0xfxfxgxx−=，0x时，函数()gx单调递增，g（3）g（2），即(2)(3)23ff，即3(2)f

2(3)f，故选：A27．A【分析】求导可得()fx解析式，原题等价于2ax−…在)1,x+上恒成立，计算即可得答案.【详解】由题意得()2afxx=+因为函数()fx在)1,+上单调递增，所以20ax+…，即2ax−

…在)1,x+上恒成立，所以2a−…，即实数a的最小值为2−.故选：A28．AC【分析】利用导数研究函数的单调性，结合单调性即可判断零点个数，根据导数的几何意义，以及奇偶性的定义，对每个选项进行逐一分析，即可判断和选择.【详解】对A：()ln(1)fxxx=+

，定义域为()1,−+，则()fx()ln11xxx=+++，由()1ln1,111xyxyxx=+==−++都在()1,−+单调递增，故y=()fx也在()1,−+单调递增，又(0)f0=，故当()1,0x−时，()fx0，()fx单调递减；当()0,x+时，

()fx0，()fx单调递增；故A正确；对B：由A知，()fx在()1,0−单调递减，在()0,+单调递增，又()00f=，故()fx只有一个零点，B错误；对C：1()2f−1ln11ln22=−=−−，根据导数几何意义可知，

C正确；对D：()fx定义域为()1,−+，不关于原点对称，故()fx是非奇非偶函数，D错误.故选：AC.29．AD【分析】由导数的图象，分析原函数的图象，根据原函数图象判断AB选项，根据图象的凹凸性判断CD选项.【详解】由导函数图象可知，()0fx

，且其绝对值越来越小，因此函数()fx的图象在其上任一点处的切线的斜率为负，并且从左到右，切线的倾斜角是越来越大的钝角，由此可得()fx的图象大致如图所示．选项A、B中，由()fx的图象可知其割线斜率()()1212fxfxxx−−恒为负数，即

12xx−与()()12fxfx−异号，故A正确，B不正确；选项C、D中，122xxf+表示122xxx+=对应的函数值，即图中点B的纵坐标，()()122fxfx+表示1xx=和2xx=所对应的函数值的平均

值，即图中点A的纵坐标，显然有()()121222fxfxxxf++，故C不正确，D正确．故选：AD．30．AD【分析】构造函数()()lnfxgxxx==，根据其单调性可判断A，构造函数()()hxfxx=+可判断B

，构造函数()()xfxx=−可判断C，当ln1x−时，函数()fx单调递增，然后可得()()()21210xxfxfx−−，然后结合A可判断D.【详解】设()()lnfxgxxx==，函数()gx单调递增，∵120xx，

∴()()21gxgx，即()()2121fxfxxx，∴()()1221xfxxfx，A正确；设()()hxfxx=+，∴()ln2hxx=+，()hx不是恒大于等于零，B错误；设()()xfxx=−，则()lnxx=，()x不是恒小于等于零，C错误；∵ln1x

−，∴()ln10fxx=+，函数()fx单调递增，∴()()()()()()()2121112221120xxfxfxxfxxfxxfxxfx−−=+−−，∴()()()()11222112xfxxfxxfxxfx+

+，又()()1221xfxxfx，∴()()()1122212xfxxfxxfx+，D正确．故选：AD．31．ABD【分析】利用导数与函数的单调性的关系可判断AB，利用函数的单调性解不等式判断CD.【详解】对于A，因为()1

fx，所以()fx为增函数，故A正确；对于B，由()()gxfxx=−，()()10gxfx=−，所以()gx为增函数，故B正确；对于C，()34f=，则()214fx−等价于()()213fxf−，又()

fx为增函数，所以213x−，解得2x，所以()214fx−的解集为()2,+，故C错误；对于D，()212fxx−等价于()()()2121133fxxf−−−=−，即()()213gxg−

，又()gx为增函数，所以213x−，解得2x，所以()212fxx−的解集为()2,+，故D正确；故选：ABD.32．BC【分析】对于AB，利用导函数的正负决定原函数的单调性分析判断即可，对于CD，根据图象求解即可【详解】对于AB，若n是()fx的图象，则当0

2x时，()0fx，则()fx在(0,2)上递减，与曲线m在(0,2)上不单调相矛盾，所以n是()fx的图象，m是()fx的图象，所以A错误，B正确，对于CD，由()()02fxfxx，得0102xx，解得01x，所以不等式组的解集

为()0,1，所以C正确，D错误，故选：BC33．BD【分析】()()()2gxfxfx=+，求导后确定出函数的单调性，由单调性判断AB，利用函数单调性的性质判断CD．【详解】令函数()()()2gxfxfx=+，则()()()210gxfxfx=

+，则()gx在R上单调递增．当ab时，()()()()()()()()()()2210gagbfafafbfbfafbfafb−=+−−=−++；当ab时，()

()()()()()()()()()2210gagbfafafbfbfafbfafb−=+−−=−++．A不正确，B正确．()()()2fxgxfx=−，()gx是增函数，若()fx是增函数，则()2fx的单调性不确定；若()fx是减函数，则()2

fx是增函数．C不正确，D正确．故选：BD．34．()2,+【分析】首先构造函数()()exfxgx=，根据题意得到()gx在R上为增函数，再将()()42e34exfxfx−转化为()()34gxgx−求解即可.【详解】

设()()exfxgx=，()()()exfxfxgx=−，因为()()0fxfx−，所以()0gx，即()gx在R上为增函数.()()()()()()422433434e34eeee4ex

xxxfxfxfxfxfxfx−−−−()()34gxgx−.因为()gx在R上为增函数，所以34xx−，解得2x.故答案为：()2,+35．)[2,02,−+．【分析】由2()()xfxfxx−＜0，构造函数()()fxhxx=，分析奇偶性，单调性，不等式2(

)0xfx≤等价于3()0xhx，即可得出答案.【详解】由2()()0xfxfxx−，构造函数()()fxhxx=，因为()fx是定义在R上的奇函数，所以()hx为偶函数，又当0x时，()hx为减函数，且(2)(2)02fh==，因为()0hx，解

得22,0xx−，由()0hx，解得<2x−或2x，不等式2()0xfx≤等价于3()0xhx，即30()0xhx或30()0xhx，解得20x−或2x，故答案为：)[2,02,−+．36．1【分析】由题意求导()1fxax=−，

化单调性为导数的正负问题，再参变分离利用不等式即可求出答案.【详解】()lnfxaxx=−Q，()1fxax=−，函数()lnfxaxx=−在()1,x+是严格增函数，10ax−在()1,x

+上恒成立，即1ax在()1,x+上恒成立，()1,x+，101x，1a时1ax在()1,x+上恒成立，实数a的最小值为：1.故答案为：1.37．(,3−−【分析】根据()gx在()2,1−−内为减函数，()0g

x在()2,1−−内恒成立求解.【详解】解：()22gxxax=−+，∵()gx在()2,1−−内为减函数，∴220xax−+在()2,1−−内恒成立，∴()()2010gg−−，即4220120aa++++，解得3a−．所以实数a的取值范围是(,3−−．

故答案为：(,3−−．38．2(,2),3−−+【分析】判断出函数的奇偶性，利用导数以及放缩法得出函数的单调性，将不等式化简，计算出不等式的解集．【详解】函数()eecosxxfxx−=++的定义域为R，且()()ee+cosxxfx

xfx−−=+=，则()fx是偶函数，()eesinxxfxx−=−−，且()eesin()xxfxxfx−−=−=−+，()fx是奇函数，又()eecos2eecos2cos+0xxxxfxxxx−−=−−=−，即()fx是为增函数，当

0x时，()(0)0fxf=，即()fx在()0,+上为增函数，则不等式(2)(2)fmfm−等价于(2)(2)fmfm−，22mm−，平方得23440mm+−，化简得()()2320mm+−，解得23m或2

m−，故答案为：2(,2),3−−+39．3−【分析】分析可知不等式2210xax++的解集为1,12，利用韦达定理可求得实数a的值.【详解】函数()fx的定义域为()0,+，且()21212xaxfxxaxx++=++=，由题意可知，不

等式2210xax++的解集为1,12，所以，1122a+=−，解得3a=−.故答案为：3−.40．(1)15ab==−；(2)单调递增区间为(,4),(1,)−−+，单调递减区间为(4,1)−.【分析】（1）求出函数的导函数，

依题意()()0405ff=−=−，即可得到方程组，解得即可；（2）由（1）可得()fx的解析式，即可得到导函数，再解关于导函数的不等式即可求出函数的单调区间.（1）解：因为()()2exfxxaxb=++，所以()2()(2)eexxfxxaxaxb=++

++2(2)exxaxab=++++，由题意可知()()0405fabfb=+=−==−，解得15ab==−；（2）解：由（1）可得()2()5e,Rxfxxxx=+−，()(

)22()(21)e5e34e(4)(1)exxxxfxxxxxxxx=+++−=+−+−=，令()0fx，解得<4x−或1x，令()0fx，解得41x−，故()fx的单调递增区间为(,4)−−，(1,)+，

()fx的单调递减区间为(4,1)−.41．(1)递减区间是(0,1)，递增区间是(1,)+；(2)0a.【分析】（1）求出导函数，利用导数的正负解不等式即可求得()fx的单调区间.（2）由函数()gx在[1,)+上为严格增函数，列

出恒成立的不等式求解作答.（1）当2a=−时，2()2lnfxxx=−的定义域为(0,)+，22(1)(1)()2xxfxxxx+−=−=，当01x时，()0fx，当1x时，()0fx，所以函数()fx的递减区间是(0,

1)，递增区间是(1,)+.（2）依题意，22()lngxxaxx=++，求导得：22()2agxxxx=+−，因函数()gx在[1,)+上为严格增函数，则[1,)x+，2222()0202agxaxxxxx+−−，显然函数222yxx=−

在[1,)+上单调递减，当1x=时，max0y=，则0a，所以实数a的取值范围是0a.42．(1)3ey=(2)答案见解析【分析】（1）求导后根据导数的几何意义求解即可；（2）求导后可得()()()21exf

xaxx=−−，再根据导函数两根的大小关系分类讨论分析单调性即可(1)当1a=时，()2()57xfxxxe=−+，则()()232exfxxx=−+，故()10f=，且()13ef=，故()fx在点()1,(1)f处的切线方程为3ey=(2)求导可得()()()(

)222e21exxfxaxaxaxx=−++=−−，当0a=时，()()21exfxx−−=，故当1x时()0fx¢>，()fx单调递增；当1x时()0fx，()fx单调递减；当0a时，令()0fx=，则11x=，22xa=1.当a<0时，21xx，故当2,xa

−和()1,+时，()0fx，()fx单调递减；当2,1xa时，()fx单调递增；2.当0a时：①当21a，即02a时，在(,1)−，2,a+上()0fx¢>，()fx单调递增；在21,a上()0fx，()

fx单调递减；②当21a=，即2a=时，()0fx，()fx在定义域R单调递增；③当21a，即2a时，在2,a−，(1,)+上()0fx¢>，()fx单调递增；在2,1a上()0fx，()fx单调递减；综上

有：当a<0时，()fx在2,a−，(1,)+单调递减，2,1a单调递增．当0a=时，()fx在(,1)−单调递增，(1,)+单调递减．当02a时，()fx在(,1)−，2,a+单调递增，21,a单调递减．当2a

=，()fx在定义域R单调递增．当2a时，()fx在2,a−，(1,)+单调递增，2,1a单调递减．43．(1)减区间为(0,2)，增区间为(2,)+，极小值为2ln2−，无极大值(2)1a

−【分析】（1）先求导，从而得到单调区间，根据单调性可得极值；（2）由条件可知()0fx恒成立，再分离变量求最值即可求解.（1）函数()fx的定义域为()0,+，当1a=时，()212ln2f

xxxx=−−求导得()21fxxx=−−，整理得：()()()21xxfxx−+=.由()0fx¢>得2x；由()0fx得02x从而，函数()fx减区间为(0,2)，增区间为(2,)+所以函数()fx极小值为()22ln2f=−，无极大值.（2）由已知)1,x

+时，()0fx恒成立，即20xax−−恒成立，即2axx−恒成立，则min2axx−.令函数()()21gxxxx=−，由()2210gxx=+知()gx在)1,+单调递增，从而()()min11agxg==−

.经检验知，当1a=−时，函数()fx不是常函数，所以a的取值范围是1a−.44．(1)4250xy+−=(2)()fx在()0,a上单调递减，在(),a+上单调递增.【分析】（1）由导数求出斜率、切点坐标可得答案；（2）求出()fx，分0a、0a讨论可得答案.（1）当2a=时，

()212ln12fxxxx=−−+，则()112f=，∴2()1fxxx=−−，∴()12f=−，所以曲线()yfx=在1x=处的切线方程为()1212yx−=−−，即4250xy+−=.（2）函数()fx的定义域为()0,+，()()()()

()2111+−−−+=−+−==xaxaxaxafxxaxxx①当0a时，恒成立，则()fx在()0,+上单调递增；②当0a时，由()0fx得xa，由()0fx得0xa，所以()fx在()0,a上单调递减，在(),a+上单调递增.